Question

If the value of $\sin \alpha =\dfrac{3}{5}$ then find the value of
\[\begin{align}
  & \left( i \right)\sin 3\alpha \\
 & \left( ii \right)\cos 3\alpha \\
 & \left( iii \right)\tan 3\alpha \\
\end{align}\]

Answer 1

Hint: We will solve $\left( i \right)\sin 3\alpha $ by using the formula $\sin 3\theta =3\sin \theta -4{{\sin }^{3}}\theta $ and putting $\theta =3\alpha $ and using $\sin \alpha =\dfrac{3}{5}\text{ and }{{\sin }^{3}}\alpha =\dfrac{27}{125}$, to compute $\cos 3\alpha =\cos \theta $ we will use $\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}$ and finally to compute ... to get result.

Complete step-by-step answer:
Let us solve this part (i),
We are given value of $\sin \alpha =\dfrac{3}{5}$
We have a trigonometric formula as $\sin 3\alpha =3\sin \alpha -4{{\sin }^{3}}\alpha $ as $\sin \alpha =\dfrac{3}{5}$ then cubing both sides we have:
\[\Rightarrow \sin 3\alpha ={{\left( \dfrac{3}{5} \right)}^{3}}=\dfrac{27}{125}\]
So, by applying above stated formula and substituting values, we get:
\[\begin{align}
  & \Rightarrow \sin 3\alpha =3\sin \alpha -4{{\sin }^{3}}\alpha \\
 & \Rightarrow \sin 3\alpha =3\left( \dfrac{3}{5} \right)-4\left( \dfrac{27}{125} \right) \\
 & \Rightarrow \sin 3\alpha =\dfrac{9}{5}-\dfrac{108}{125} \\
 & \Rightarrow \sin 3\alpha =\dfrac{25\times 9-108}{125} \\
 & \Rightarrow \sin 3\alpha =\dfrac{117}{125} \\
\end{align}\]
Therefore, the value of \[\left( i \right)\sin 3\alpha =\dfrac{117}{125}\]
Consider part (ii) we have,
Let $3\alpha =\theta $ then $\sin \theta =\dfrac{117}{125}$ and we have to compute $\cos \theta $
Consider triangle ABC as below with $\angle C\text{ as }\theta $

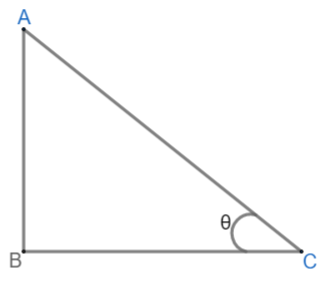
Then, as \[\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}\text{ and }\sin \theta =\dfrac{117}{125}\]
Perpendicular AB = 117 and Hypotenuse AC = 125.
Now, we will compute side BC of triangle ABC by using Pythagoras theorem stated as below:
In a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of other two sides.
In $\Delta ABC$
\[\begin{align}
  & {{\left( AC \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}} \\
 & {{\left( 125 \right)}^{2}}={{\left( 117 \right)}^{2}}+{{\left( BC \right)}^{2}} \\
 & {{\left( BC \right)}^{2}}={{\left( 125 \right)}^{2}}+{{\left( 117 \right)}^{2}} \\
 & B{{C}^{2}}=15625-13689 \\
 & B{{C}^{2}}=1936 \\
 & BC=44 \\
\end{align}\]
So length of side BC = 44.
Now, we know that, \[\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}\]
\[\begin{align}
  & \cos \theta =\dfrac{\text{Base}\to \text{BC}}{\text{Hypotenuse}\to \text{AC}} \\
 & \cos \theta =\dfrac{\text{44}}{\text{125}} \\
\end{align}\]
The value of \[\left( ii \right)\cos 3\alpha =\dfrac{44}{125}\]
Finally we compute $\tan \theta $ by using formula $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$
\[\text{as }\theta =3\alpha \Rightarrow \tan 3\alpha =\dfrac{\sin 3\alpha }{\cos 3\alpha }\]
Substituting the values of \[\sin 3\alpha \text{ as }\dfrac{117}{125}\text{ and }\cos 3\alpha \text{ as }\dfrac{44}{125}\]
\[\begin{align}
  & \tan 3\alpha =\dfrac{\dfrac{117}{125}}{\dfrac{44}{125}} \\
 & \tan 3\alpha =\dfrac{117}{44} \\
\end{align}\]
The value of \[\left( iii \right)\tan 3\alpha =\dfrac{117}{44}\]
Hence, our answer is:
\[\begin{align}
  & \left( i \right)\sin 3\alpha =\dfrac{117}{125} \\
 & \left( ii \right)\cos 3\alpha =\dfrac{44}{125} \\
 & \left( iii \right)\tan 3\alpha =\dfrac{117}{44} \\
\end{align}\]

Note: Another way to calculate value of $\cos 3\alpha $ from $\sin 3\alpha $ is by using the trigonometric formula $\sin \theta =\sqrt{1-{{\cos }^{2}}\theta }$
\[\begin{align}
  & \sin 3\alpha =\dfrac{117}{125} \\
 & \Rightarrow \sqrt{1-{{\cos }^{2}}3\alpha }=\dfrac{117}{125} \\
 & \Rightarrow 1-{{\cos }^{2}}3\alpha ={{\left( \dfrac{117}{125} \right)}^{2}}=\dfrac{13689}{15625} \\
 & \Rightarrow {{\cos }^{2}}3\alpha =1-\dfrac{13689}{15625}=\dfrac{15625-13689}{15625} \\
 & \Rightarrow \cos 3\alpha =\dfrac{44}{125} \\
\end{align}\]
Which is the correct value.