Question

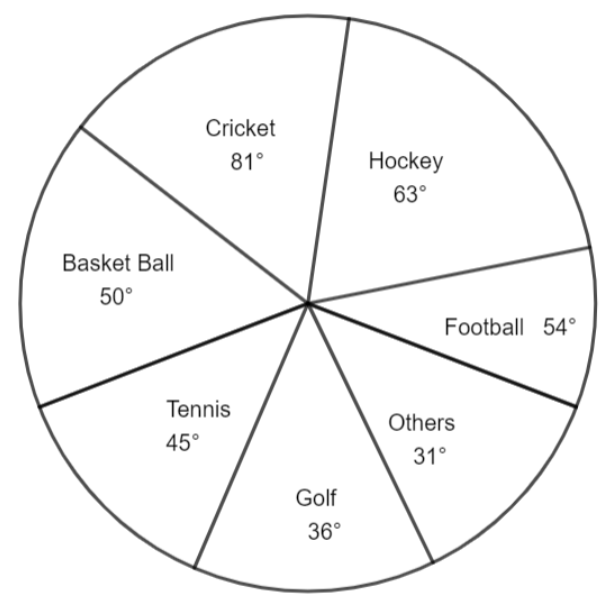
If the total amount spent on sports during the year be Rs. 1,80,00,000, the amount spent on Basketball exceeds on Tennis by;

Answer 1

Hint: To solve this question, firstly we will add a degree measure of all sports shown in the pie chart. After that, we will find the amount of money spent on Basketball and Tennis respectively. Then, to find the amount by which Basketball exceeds on Tennis, we will subtract the amount of tennis from the amount spent on basketball.

Complete step-by-step solution:
Now, from the pie chart first step is to find out how much amount of money does the degree a sector is acquiring for each sport which can find out by simple formula which is a degree of sports to the summation of a degree of all sports put together multiplied by the total amount given for all sports that are \[\dfrac{\text{degree of particular sport}}{\text{degree of all of the sports put together}}\text{ }\!\!\times\!\!\text{ 1,80,00,000}\].
Now, the summation of degree measure for all sports is equal to a degree acquired by basketball + degree acquired by tennis + degree acquired by golf + degree acquired by football + degree acquired by hockey + degree acquired by cricket + degree acquired by other sports.
So, summation of degree measure for all sports = ${{50}^{\circ }}+{{81}^{\circ }}+{{63}^{\circ }}+{{54}^{\circ }}+{{31}^{\circ }}+{{36}^{\circ }}+{{45}^{\circ }}$
On simplifying, we get
Summation of degree measure for all sports = \[{{360}^{\circ }}\]
Now, Amount given for sport Basketball = \[\dfrac{\text{degree of basketball}}{\text{degree of all of sports put together}}\text{ }\!\!\times\!\!\text{ 1,80,00,000}\]
On putting value, we get
\[=\dfrac{50}{360}\text{ }\!\!\times\!\!\text{ 1,80,00,000}\]
On simplifying, we get
\[=\dfrac{5}{36}\text{ }\!\!\times\!\!\text{ 1,80,00,000}\]
= 25,00,000
Similarly, Amount given for sport Tennis = \[\dfrac{\text{degree of tennis}}{\text{degree of all of sports put together}}\text{ }\!\!\times\!\!\text{ 1,80,00,000}\]
On putting value, we get
\[=\dfrac{45}{360}\text{ }\!\!\times\!\!\text{ 1,80,00,000}\]
On simplifying, we get
\[=\dfrac{1}{8}\text{ }\!\!\times\!\!\text{ 1,80,00,000}\]
= 22,50,000
So, the amount spent on Basketball exceeds on Tennis by,
Rs. 25,00,000 – Rs. 22,50,000
On simplifying, we get
Rs. 2,50,000
So, the amount spent on Basketball exceeds on Tennis by Rs. 2,50,000.

Note: Total amount of money spent on any of the sports should be measured properly as it will change the value of spent money. Also, to find the difference between the amount spent on basketball and tennis, the calculation must be according to the statement of the question that is don’t subtract the amount of basketball from the amount of tennis as this will give an amount in negative. Try not to make any calculation mistakes. Also, you can represent the pie chart in terms of the amount spent on sport rather than degree measure in the solution of the question.