Question

If the tangents on the ellipse \[4{{x}^{2}}+{{y}^{2}}=8\] at the point $\left( 1,2 \right)$ and $\left( a,b \right)$ are perpendicular to each other, then ${{a}^{2}}$ is equal to:
A. $\dfrac{64}{17}$
B. $\dfrac{2}{17}$
C. $\dfrac{128}{17}$
D. $\dfrac{4}{17}$

Answer 1

Hint: First we will start by converting the given equation of ellipse into its standard form and then we will find the equation of tangents at the given point $\left( 1,2 \right)$ and $\left( a,b \right)$ using the formula \[\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1\] ; once we find both the tangents, we will then apply the theorem of perpendicular lines and find the variables.

Complete step by step answer:
We will start by converting the given equation of ellipse into its standard form that is: \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]
Now, we have the equation of ellipse given in the question as follows: \[4{{x}^{2}}+{{y}^{2}}=8\text{ }...........\text{ Equation 1}\text{.}\]
Now we will divide the whole equation by 8 to convert it into its standard form:
\[\begin{align}
  & \Rightarrow ~\dfrac{4{{x}^{2}}}{8}+\dfrac{{{y}^{2}}}{8}=\dfrac{8}{8} \\
 & \Rightarrow \dfrac{{{x}^{2}}}{2}+\dfrac{{{y}^{2}}}{8}=1 \\
 & \Rightarrow \dfrac{{{x}^{2}}}{{{\left( \sqrt{2} \right)}^{2}}}+\dfrac{{{y}^{2}}}{{{\left( 2\sqrt{2} \right)}^{2}}}=1 \\
\end{align}\]
Now, we know that the equation of tangent to the ellipse \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\] at \[({{x}_{1}},{{y}_{1}})\] is \[\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1\]
Therefore, equation of tangent to the ellipse \[\dfrac{{{x}^{2}}}{{{\left( \sqrt{2} \right)}^{2}}}+\dfrac{{{y}^{2}}}{{{\left( 2\sqrt{2} \right)}^{2}}}=1\] at $\left( 1,2 \right)$ is : \[\begin{align}
  & \dfrac{x\left( 1 \right)}{{{\left( \sqrt{2} \right)}^{2}}}+\dfrac{y\left( 2 \right)}{{{\left( 2\sqrt{2} \right)}^{2}}}=1\Rightarrow \dfrac{x}{2}+\dfrac{y}{4}=1 \\
 & \Rightarrow \dfrac{2x+y}{4}=1\text{ }\Rightarrow 2x+y=4.........\text{ Equation 2}\text{.} \\
\end{align}\]
Similarly, the equation of tangent at $\left( a,b \right)$ will be :
 \[\begin{align}
  & \dfrac{x\left( a \right)}{{{\left( \sqrt{2} \right)}^{2}}}+\dfrac{y\left( b \right)}{{{\left( 2\sqrt{2} \right)}^{2}}}=1\Rightarrow \dfrac{ax}{2}+\dfrac{by}{8}=1 \\
 & \Rightarrow \dfrac{4ax+by}{8}=1\Rightarrow 4ax+by=8\text{ }.........\text{ Equation 3}\text{.} \\
\end{align}\]
So according to these conditions, we will have the following diagram:

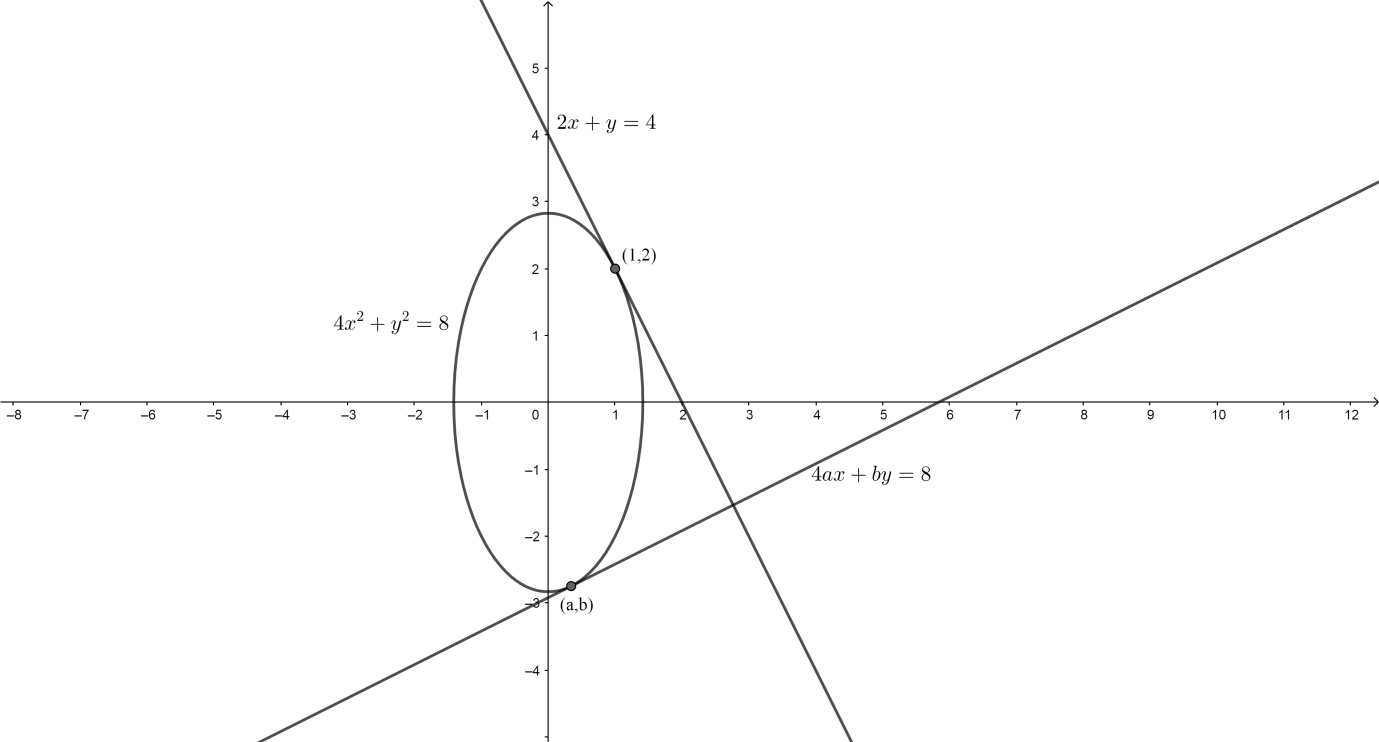
Now, it is given in the question that both the tangents at $\left( 1,2 \right)$ and $\left( a,b \right)$ are perpendicular to each other, so we will apply the following theorem:
If lines \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\ \,\text{and}\ \,{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\] are perpendicular, then \[\left( \dfrac{-{{a}_{1}}}{{{b}_{1}}} \right)\times \left( -\dfrac{{{a}_{2}}}{{{b}_{2}}} \right)=-1\] , we have with us \[2x+y=4\]and \[4ax+by=8\] , which are perpendicular to each other :
Therefore: \[\left( \dfrac{-2}{1} \right)\times \left( \dfrac{-4a}{b} \right)=-1\Rightarrow b=-8a\] Now, on squaring both sides we will get ${{b}^{2}}=64{{a}^{2}}\text{ }........\text{Equation 4}\text{.}$

Now it is given in the question that $\left( a,b \right)$ lies on the given ellipse therefore we will put these points in the equation of ellipse as seen in Equation 1 above:
 \[\begin{align}
  & 4{{x}^{2}}+{{y}^{2}}=8 \\
 & \Rightarrow 4{{\left( a \right)}^{2}}+{{\left( b \right)}^{2}}=8 \\
 & \Rightarrow 4{{a}^{2}}+{{b}^{2}}=8 \\
\end{align}\]
We will now put the value of ${{b}^{2}}$ from equation 4 in \[4{{a}^{2}}+{{b}^{2}}=8\]:
\[4{{a}^{2}}+{{b}^{2}}=8\Rightarrow 4{{a}^{2}}+64{{a}^{2}}=8\] ;
Taking out 4 common from the equation :
\[\begin{align}
  & \Rightarrow 4{{a}^{2}}+64{{a}^{2}}=8 \\
 & \Rightarrow 4\left( {{a}^{2}}+16{{a}^{2}} \right)=8 \\
 & \Rightarrow {{a}^{2}}+16{{a}^{2}}=2 \\
 & \Rightarrow 17{{a}^{2}}=2 \\
 & \Rightarrow {{a}^{2}}=\dfrac{2}{17} \\
\end{align}\]
Therefore the answer is option D.

Note:
Remember that mistakes can be made in applying the perpendicular lines theorem as there are three negative signs involved. We will get the negative value of $b$ , but we will square it as we require the square of $a$ according to the question.