Question

If the system of inequalities y ≥ 2x+1 and Y > \[\dfrac{1}{2}x - 1\] is graphed in the xy-plane above, which quadrant contains no solutions to the system?

A. Quadrant ll
B. Quadrant lll
C. Quadrant lV
D. There are solutions in all four quadrants

Answer 1

Hint: A quadrant is a quarter of a circle's circumference. a circle's diameter and the area surrounded by two perpendicular radii any of the four parts formed by the division of a plane by two coordinate axes. The plane is divided into four quadrants by the coordinate axes, which are labelled first, second, third, and fourth as shown.

Complete step-by-step answer:
Given the inequalities y ≥ 2x+1 and Y >\[\dfrac{1}{2}x - 1\].
Initially, make a graph for the equations \[y = 2x + 1\]and \[y = \dfrac{1}{2}x - 1\](refer the figure given below)
Here for \[y = 2x + 1\]
Substitute, y=0 and x=0
That is,
\[2x + 1 = 0\] \[ \Rightarrow x = - 0.5\]and \[y = 1\]
Therefore, the line y =2x+1 passes through the points (-0.5,0) and (0,1). (Refer the figure given below)
That is, y ≥ 2x+1 includes the area above the line.
Now for Y =\[\dfrac{1}{2}x - 1\].
Substitute, y=0 and x=0
That is,
\[\dfrac{1}{2}x - 1 = 0\]\[ \Rightarrow x = 2\]and \[y = 1\]
Therefore, the line \[y = \dfrac{1}{2}x - 1\] passes through the points (2,0) and (0,-1). (Refer the figure given below)
That is Y >\[\dfrac{1}{2}x - 1\] includes the area above the line.

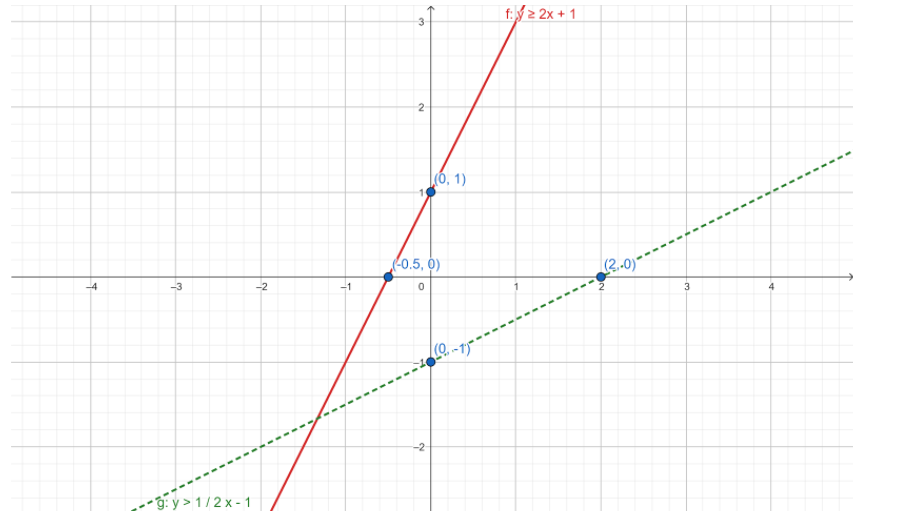
So from the above figure it is clear that I, II, and III is the intersection region.
As a result, there is no solution for quadrant IV.
So, the correct answer is “Option C”.

Note: Remember the quadrants correctly. Also follow the above mentioned steps to get the graph and quadrant. Quadrants are named in an anticlockwise direction by convention. On a Cartesian plane, a quadrant is one of the four divisions. Each quadrant contains a mix of positive and negative x and y values.