
If the system is released, then the acceleration of the centre of mass of the system is
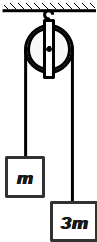
A. \[\dfrac{g}{4}\]
B. \[\dfrac{g}{2}\]
C. \[g\]
D. \[2g\]

Answer
577.8k+ views
Hint: In this question we have been asked to calculate the acceleration of centre of mass of the given pulley system. To solve this question, we shall first calculate the acceleration of the two blocks by using the equation of motion from the free body diagram. Later, using this result we shall calculate the acceleration of the centre of mass of the given system. Centre of mass is a point in space at which the whole mass of the system can be assumed to be concentrated.
Formula Used: \[{{a}_{c}}=\dfrac{{{m}_{1}}{{a}_{1}}-{{m}_{2}}{{a}_{2}}}{{{m}_{1}}+{{m}_{2}}}\]
Where,
\[{{a}_{c}}\] is the acceleration of centre of mass
\[{{m}_{1}}\] and \[{{m}_{2}}\] is the mass of the two blocks
\[{{a}_{1}}\] and \[{{a}_{2}}\] is the acceleration of blocks
Complete answer:
The FBD for the given pulley mass system will be as shown in the figure, below.
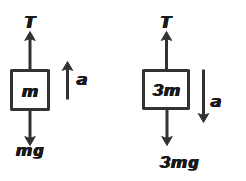
Therefore, from the above figure we can write,
\[T-mg=ma\] ……………… (1)
Similarly,
\[3mg-T=3ma\] …………….. (2)
Therefore, from (1) and (2)
We get,
\[2mg=4ma\]
Let us assume,
\[g=10\] ……………. (A)
Therefore,
\[a=5m/{{s}^{2}}\]
Now we know that, acceleration of centre of mass of system is given by,
\[{{a}_{c}}=\dfrac{{{m}_{1}}{{a}_{1}}-{{m}_{2}}{{a}_{2}}}{{{m}_{1}}+{{m}_{2}}}\]
Where,
\[{{a}_{1}}={{a}_{2}}=5\]
After substituting the values,
We get,
\[{{a}_{c}}=\dfrac{5\left( 3m-m \right)}{m+3m}\]
Therefore,
\[{{a}_{c}}=\dfrac{10}{4}\]
Now from (A) we can say that,
\[{{a}_{c}}=\dfrac{g}{4}\]
Therefore, the correct answer is option A.
Note:
The centre of mass can be calculated by taking the masses and multiplying them by their positions from the selected point of origin and dividing them by the total mass of the system. The centre of mass is a point on which the force is applied; it causes linear acceleration without an angular acceleration. The concept of centre of mass was introduced by Archimedes.
Formula Used: \[{{a}_{c}}=\dfrac{{{m}_{1}}{{a}_{1}}-{{m}_{2}}{{a}_{2}}}{{{m}_{1}}+{{m}_{2}}}\]
Where,
\[{{a}_{c}}\] is the acceleration of centre of mass
\[{{m}_{1}}\] and \[{{m}_{2}}\] is the mass of the two blocks
\[{{a}_{1}}\] and \[{{a}_{2}}\] is the acceleration of blocks
Complete answer:
The FBD for the given pulley mass system will be as shown in the figure, below.

Therefore, from the above figure we can write,
\[T-mg=ma\] ……………… (1)
Similarly,
\[3mg-T=3ma\] …………….. (2)
Therefore, from (1) and (2)
We get,
\[2mg=4ma\]
Let us assume,
\[g=10\] ……………. (A)
Therefore,
\[a=5m/{{s}^{2}}\]
Now we know that, acceleration of centre of mass of system is given by,
\[{{a}_{c}}=\dfrac{{{m}_{1}}{{a}_{1}}-{{m}_{2}}{{a}_{2}}}{{{m}_{1}}+{{m}_{2}}}\]
Where,
\[{{a}_{1}}={{a}_{2}}=5\]
After substituting the values,
We get,
\[{{a}_{c}}=\dfrac{5\left( 3m-m \right)}{m+3m}\]
Therefore,
\[{{a}_{c}}=\dfrac{10}{4}\]
Now from (A) we can say that,
\[{{a}_{c}}=\dfrac{g}{4}\]
Therefore, the correct answer is option A.
Note:
The centre of mass can be calculated by taking the masses and multiplying them by their positions from the selected point of origin and dividing them by the total mass of the system. The centre of mass is a point on which the force is applied; it causes linear acceleration without an angular acceleration. The concept of centre of mass was introduced by Archimedes.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




