Question

If the supplement of an angle is ${{65}^{\circ }}$. Then find the complement angle.

Answer 1

Hint: We first define the definitions of complement and supplement angles. Based on the given angle we find the supplement angle. Using binary operations, we try to find the complement angles of that solution. We need to check if the solution of the complement angle is positive or negative.

Complete step-by-step solution
The terms supplement and complement are the relations between two angles.
If the sum of two angles is equal to ${{90}^{\circ }}$, then the angles are complementary angles to each other. If the sum is equal to ${{180}^{\circ }}$, then the angles are supplementary angles to each other.
Let’s assume x and y are complementary angles to each other which means $x+y={{90}^{\circ }}$.
And if x and y are supplementary angles to each other which means $x+y={{180}^{\circ }}$.
For our given problem we assume the angle as $\alpha $. So, $\alpha ={{65}^{\circ }}$.
Let the supplement angle of $\alpha $ be $\beta $. This implies $\alpha +\beta ={{180}^{\circ }}$.

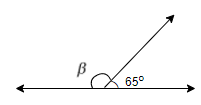
We place the value of $\alpha $ in $\alpha +\beta ={{180}^{\circ }}$.
$\begin{align}
  & \Rightarrow \alpha +\beta ={{180}^{\circ }} \\
 & \Rightarrow {{65}^{\circ }}+\beta ={{180}^{\circ }} \\
 & \Rightarrow \beta ={{180}^{\circ }}-{{65}^{\circ }}={{115}^{\circ }} \\
\end{align}$
So, the angle is ${{115}^{\circ }}$.
Now we need to find the complement angle of ${{115}^{\circ }}$.
Let the angle be $\gamma $. This implies $\beta +\gamma ={{90}^{\circ }}$.
We place the value of $\beta $ in $\beta +\gamma ={{90}^{\circ }}$.
$\begin{align}
  & \Rightarrow \beta +\gamma ={{90}^{\circ }} \\
 & \Rightarrow {{115}^{\circ }}+\gamma ={{90}^{\circ }} \\
 & \Rightarrow \gamma ={{90}^{\circ }}-{{115}^{\circ }}=-{{25}^{\circ }} \\
\end{align}$
The value of the angle can’t be negative.
So, there exists no such angle for which its complement angle will be ${{115}^{\circ }}$.
It has no complement angle. It doesn’t exist.

Note: We learned that if the sum of two angles is equal to ${{90}^{\circ }}$, then the angles are complementary angles to each other. This means we can’t find complementary angles of the angles valued more than ${{90}^{\circ }}$. Similar thing for supplement angles. We can’t find complementary angles of the angles valued more than ${{180}^{\circ }}$.