Question

If the sum of a pair of opposite angles of a quadrilateral is $180{}^\circ $, then show that the quadrilateral is cyclic.

Answer 1

Hint: We are going to solve this problem in a different manner i.e. we will show the sum of either pair of opposite angles of a cyclic quadrilateral is $180{}^\circ $. From this, we can say “If the sum of a pair of opposite angles of a quadrilateral is $180{}^\circ $, then the quadrilateral is cyclic”. To find the sum of either pair of opposite angles of a cyclic quadrilateral we will assume a cyclic quadrilateral along with its diagonals. Now we will obtain a relation between the internal angles using circle rules i.e. the angles that are in the same segments are equal. Now we will use these relations and try to find the sum of the angles of the quadrilateral and equate it to $360{}^\circ $ and get the required relation i.e. sum either pair of opposite angles are equal to $180{}^\circ $.

Complete step-by-step solution:
Let us assume a cyclic quadrilateral $ABCD$ as shown in the below figure.

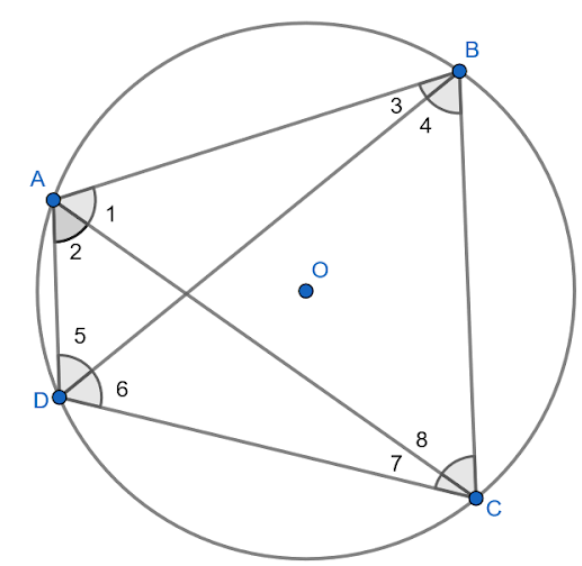
Here we need to prove the sum of pair of opposite angles of cyclic quadrilateral is $180{}^\circ $, from the above figure we can write it mathematically as
$\angle BAD+\angle BCD=180{}^\circ $ or $\angle ABC+\angle ADC=180{}^\circ $
From the diagram we can write the relation between the internal angles $\angle 1,\angle 2,\angle 3,\angle 4,\angle 5,\angle 6,\angle 7,\angle 8$ as given below
From the Chord $AB$, we can write $\angle 5=\angle 8....\left( \text{i} \right)$ [Angles in same segment are equal].
From the Chord $BC$, we can write $\angle 1=\angle 6....\left( \text{ii} \right)$ [Angles in the same segment are equal].
From the Chord $CD$, we can write $\angle 2=\angle 4....\left( \text{iii} \right)$ [Angles in the same segment are equal].
From the Chord $AD$, we can write $\angle 7=\angle 3....\left( \text{iv} \right)$ [Angles in the same segment are equal].
We know that the sum of angles in a quadrilateral is $360{}^\circ $, hence we can write
$\angle BAD+\angle ABD+\angle BCD+\angle ADC=360{}^\circ $
From the diagram we can write $\angle BAD=\angle 1+\angle 2,\angle ABD=\angle 3+\angle 4,\angle BCD=\angle 7+\angle 8,\angle ADB=\angle 5+\angle 6$
Substituting above values in the sum of angles of quadrilateral, then we will get
$\begin{align}
  & \angle BAD+\angle ABD+\angle BCD+\angle ADC=360{}^\circ \\
 &\Rightarrow \angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6+\angle 7+\angle 8=360{}^\circ \\
\end{align}$
Rearranging the above angles so that the opposite angles are at one place, then
$\left( \angle 1+\angle 2+\angle 7+\angle 8 \right)+\left( \angle 3+\angle 4+\angle 5+\angle 6 \right)=360{}^\circ $
From equations $\left( \text{i} \right),\left( \text{ii} \right),\left( \text{iii} \right),\left( \text{iv} \right)$, substituting the values of $\angle 3,\angle 4,\angle 5,\angle 6$ in the above equation, then we will get
$\begin{align}
  & \left( \angle 1+\angle 2+\angle 7+\angle 8 \right)+\left( \angle 3+\angle 4+\angle 5+\angle 6 \right)=360{}^\circ \\
 &\Rightarrow \left( \angle 1+\angle 2+\angle 7+\angle 8 \right)+\left( \angle 7+\angle 2+\angle 8+\angle 1 \right)=360{}^\circ \\
 &\Rightarrow \left( \angle 1+\angle 2+\angle 7+\angle 8 \right)+\left( \angle 1+\angle 2+\angle 7+\angle 8 \right)=360{}^\circ \\
\end{align}$
We know that $a+a=2a$, then
$2\left( \angle 1+\angle 2+\angle 7+\angle 8 \right)=360{}^\circ $
Dividing the above equation with $2$ on both sides, then we will get
$\begin{align}
  & \left( \angle 1+\angle 2+\angle 7+\angle 8 \right)=180{}^\circ \\
 & \left( \angle 1+\angle 2 \right)+\left( \angle 7+\angle 8 \right)=180{}^\circ \\
\end{align}$
From the diagram the value of $\angle 1+\angle 2=\angle BAD$, $\angle 7+\angle 8=\angle BCD$, then
$\begin{align}
  & \left( \angle 1+\angle 2 \right)+\left( \angle 7+\angle 8 \right)=180{}^\circ \\
 &\Rightarrow \angle BAD+\angle BCD=180{}^\circ \\
\end{align}$
Similarly,
$\angle ABC+\angle ADC=180{}^\circ $
From this we can say that in a cyclic quadrilateral the sum of pair of opposite angles is equal to $180{}^\circ $ or If the sum of pair of opposite angles in a quadrilateral is equal to $180{}^\circ $, then the quadrilateral is cyclic quadrilateral.

Note: Here the problem is completely based on the cyclic quadrilateral. A cyclic quadrilateral is nothing but a quadrilateral whose vertices lie on the same circle. In the problem we have substitute the values of $\angle 3,\angle 4,\angle 5,\angle 6$ from equations $\left( \text{i} \right),\left( \text{ii} \right),\left( \text{iii} \right),\left( \text{iv} \right)$. We can also substitute the values of $\angle 1,\angle 2,\angle 7,\angle 8$ from same equations $\left( \text{i} \right),\left( \text{ii} \right),\left( \text{iii} \right),\left( \text{iv} \right)$, then we will get
$\begin{align}
  & \Rightarrow \left( \angle 1+\angle 2+\angle 7+\angle 8 \right)+\left( \angle 3+\angle 4+\angle 5+\angle 6 \right)=360{}^\circ \\
 & \Rightarrow \left( \angle 3+\angle 4+\angle 5+\angle 6 \right)+\left( \angle 3+\angle 4+\angle 5+\angle 6 \right)=360{}^\circ \\
 & \Rightarrow 2\left( \angle 3+\angle 4+\angle 5+\angle 6 \right)=360{}^\circ \\
 & \Rightarrow \angle 3+\angle 4+\angle 5+\angle 6=180{}^\circ \\
\end{align}$
From diagram we can write
$\angle ABC+\angle ADC=180{}^\circ $