Question

If the side of a square is increased by 30%, then the area is increased by:
(a) 9%
(b) 27%
(c) 30%
(d) 69%

Answer 1

Hint: Start by letting the length of the side of the old square be a units. If you add 30% of ‘a’ to ‘a’, we get the side length of the new square that is formed by increasing the side length by 30%. We know that the area of a square is equal to the square of its side, so find the area of the new and old square and find the difference. Find the percentage of the difference with respect to the area of the old square to get the % increase in area.

Complete step-by-step answer:
Let us start the solution by letting the length of the sides of the old square is a unit and the side length of the new square formed after increasing the length by 30% to be ‘x’ units. These can be diagrammatically represented as:

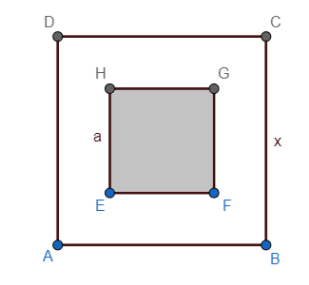
Now, if we add 30% of ‘a’ to ‘a’, we get the side length ‘x’ of the new square that is formed by increasing the side length by 30%.
$x=a+\dfrac{30}{100}a=\dfrac{13}{10}a$
Now we know that the area of the square is equal to half of the square of the length of the diagonal of the square.
$\therefore \text{ Area of the old square = }{{a}^{2}}$
$\therefore \text{ Area of the new square = }{{x}^{2}}={{\left( \dfrac{13a}{10} \right)}^{2}}=\dfrac{169{{a}^{2}}}{100}$
So, the increase in area is given by the difference between the two areas, i.e., the area of the new square minus the area of the old square.
$\text{Area increased}=\dfrac{169}{100}{{a}^{2}}-{{a}^{2}}=\dfrac{169{{a}^{2}}-100{{a}^{2}}}{100}=\dfrac{69}{100}{{a}^{2}}$
Now, the percentage of the difference with respect to the area of the old square is the % increase in area.
$\%\text{ increase in area}=\dfrac{\dfrac{69}{100}{{a}^{2}}}{{{a}^{2}}}\times 100=\dfrac{69{{a}^{2}}}{100{{a}^{2}}}\times 100=69%$
Hence, the answer to the above question is option (d).


Note: Remember that % increase must always be calculated with respect to the area of the original figure, in our case the old square and not with respect to the derived figures. Also, making a diagram helps a lot in understanding and interpreting the problem, so always keep a habit of drawing the figures in such questions.