Question

If the resultant of \[3\overrightarrow{p}\] and \[4\overrightarrow{p}\] is a force \[5\overrightarrow{p}\], then the angle between \[3\overrightarrow{p}\] and \[5\overrightarrow{p}\] is
a. \[{{\sin }^{-1}}\left( \dfrac{3}{5} \right)\]
b. \[{{\sin }^{-1}}\left( \dfrac{4}{5} \right)\]
c. \[{{90}^{\circ }}\]
d. None of these

Answer 1

Hint: First we will put the values in the resultant formula. Now using this we will find the angle made between the resultant and the forces \[3\overrightarrow{p}\] and \[5\overrightarrow{p}\]. Take angle between \[4\overrightarrow{p}\] and \[5\overrightarrow{p}\] as \[\beta \], \[\alpha \] between \[5\overrightarrow{p}\] and \[3\overrightarrow{p}\]. So, we have the total angle \[\phi =\alpha +\beta \].

Complete step by step answer:
Now consider the figure drawn below,

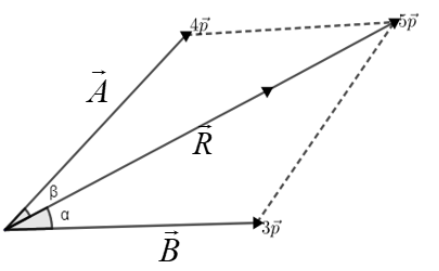
Now the force \[4\overrightarrow{p}\] and force \[3\overrightarrow{p}\] is drawn and the resultant of these two forces is \[5\overrightarrow{p}\] force.
Let the angle made between the \[4\overrightarrow{p}\] force and resultant \[5\overrightarrow{p}\] is \[\beta \] and the angle made between the \[3\overrightarrow{p}\] force and resultant \[5\overrightarrow{p}\] is \[\alpha \].
We know the basic formula where the resultant between 2 vectors \[\overrightarrow{A}\] and \[\overrightarrow{B}\] is given by the equation,
\[{{R}^{2}}={{A}^{2}}+{{B}^{2}}+2AB\cos \phi \]
Let us substitute the value into the equation, Hence we havr resultant \[=R=5\overrightarrow{p}\] \[A=4\overrightarrow{p}\] and \[B=3\overrightarrow{p}\]
Put ,\[\phi =\alpha +\beta \] in the above expression.
\[\begin{align}
  & \Rightarrow {{\left( 5\overrightarrow{p} \right)}^{2}}={{\left( 4\overrightarrow{p} \right)}^{2}}+{{\left( 3\overrightarrow{p} \right)}^{2}}+2\left( 4\overrightarrow{p} \right)\left( 3\overrightarrow{p} \right)\cos \left( \alpha +\beta \right) \\
 & \Rightarrow 25{{\overrightarrow{p}}^{2}}=16{{\overrightarrow{p}}^{2}}+9{{\overrightarrow{p}}^{2}}+24{{\overrightarrow{p}}^{2}}\cos \left( \alpha +\beta \right) \\
 & 25{{\overrightarrow{p}}^{2}}=25{{\overrightarrow{p}}^{2}}+24{{\overrightarrow{p}}^{2}}\cos \left( \alpha +\beta \right) \\
\end{align}\]
Cancel out \[25{{\overrightarrow{p}}^{2}}\] from LHS and RHS.
\[\begin{align}
  & \Rightarrow 24{{\overrightarrow{p}}^{2}}\cos \left( \alpha +\beta \right)=0 \\
 & \cos \left( \alpha +\beta \right)=0 \\
 & \Rightarrow \alpha +\beta ={{\cos }^{-1}}0\left[ \because {{\cos }^{-1}}0={{90}^{\circ }} \right] \\
 & \alpha +\beta ={{90}^{\circ }} \\
\end{align}\]
Now, from the figure we can use the sine function to bring out the relation between the resultant and the vectors using the below mentioned formula. Now we can say that $\vec{R}\sin \alpha =\vec{B}\sin \left( \alpha +\beta \right)$ which is nothing but y projection of $\vec{B}$ and $\vec{R}$. Hence we have \[\overrightarrow{B}=\dfrac{\overrightarrow{R}\sin \alpha }{\sin \left( \alpha +\beta \right)}\]
Now substituting the values of \[\overrightarrow{A}=4\overrightarrow{p},\overrightarrow{B}=3\overrightarrow{p},\alpha +\beta ={{90}^{\circ }},\overrightarrow{R}=5\overrightarrow{p}\] we get,
\[\begin{align}
  & \Rightarrow 4\overrightarrow{p}=\dfrac{5\overrightarrow{p}\sin \alpha }{\sin 90}\left[ \because \sin 90=1 \right] \\
 & \Rightarrow 4\overrightarrow{p}=\dfrac{5\overrightarrow{p}\sin \alpha }{1} \\
 & \sin \alpha =\dfrac{4\overrightarrow{p}}{5\overrightarrow{p}} \\
 & \Rightarrow \sin \alpha =\dfrac{4}{5} \\
 & \therefore \alpha ={{\sin }^{-1}}\left( \dfrac{4}{5} \right) \\
\end{align}\]

So, the correct answer is “Option b”.

Note: The angle between the resultants is taken as \[\alpha \] and \[\beta \], which makes the total angle \[\phi =\alpha +\beta \]. We can solve this in easy way by directly applying the formula,
\[\overrightarrow{B}=\dfrac{\overrightarrow{R}\sin \alpha }{\sin \left( \alpha
+\beta \right)}\].