Question

If the range is double the maximum height of projectile, then \[\theta \] is
A. \[{{\tan }^{-1}}4\]
B. \[{{\tan }^{-1}}\dfrac{1}{4}\]
C. \[{{\tan }^{-1}}1\]
D. \[{{\tan }^{-1}}2\]

Answer 1

Hint: In this question we have been asked to calculate the angle of projection, when the range is double the maximum height. To solve this question, we shall use the formulas for projectile motion of a particle. The condition given to us is that, the range the horizontal distance travelled by the particle is double the height attained by the projectile.

Formula used:
\[R=\dfrac{{{u}^{2}}\sin 2\theta }{g}\]
\[H=\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\]

Complete step by step answer:
Let us assume that a body was projected with initial velocity u at an angle \[\theta \], as shown in the figure below.
 

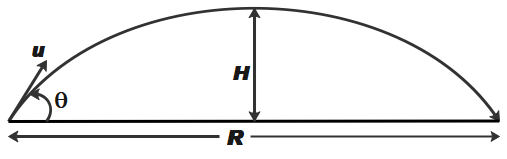
It is said that range is twice the maximum height of the projectile. Let, R be the range and H be the maximum height of the projectile.
We know that
\[R=\dfrac{{{u}^{2}}\sin 2\theta }{g}\] ………………. (1)
Also,
\[H=\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] …………….. (2)
Therefore, from given condition
\[R=2H\]
Therefore, from (1) and (2)
\[\dfrac{{{u}^{2}}\sin 2\theta }{g}=2\times \dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}\] …………. (3)
We know that,
\[\sin 2\theta =2\sin \theta \cos \theta \]
Therefore, on solving (3)
We get,
\[2\sin \theta \cos \theta =2{{\sin }^{2}}\theta \]
On solving
\[\tan \theta =2\]
Therefore,
\[\theta ={{\tan }^{-1}}2\]
Therefore, the correct answer is option D.

Note:
When an object is thrown or projected at an angle, the object follows a curved path. This path is called the trajectory of the object. The maximum horizontal covered by an object or the horizontal displacement of the object is known as range. Similarly, when the object is projected upwards at some angle, the object reaches a certain maximum height depending on the initial velocity and angle of projection.