Question

If the radius of a right circular cylinder open at both the ends is decreasing by \[25\% \] and the height of the cylinder is increased by \[25\% \], then the surface area of the cylinder thus formed is
A) Remains unaltered
B) Increased by \[25\% \]
C) Decreased by \[25\% \]
D) Decreased by \[6.25\% \]

Answer 1

Hint: In this question, we have to choose the correct option for the particular required.
The surface area of a cylinder is \[2\pi rh\] where r is the radius of the cylinder and h is the height of the cylinder.
We have to find out both the surface area of the cylinder, first taking two random variables as radius and height and then after decreasing and increasing the respective values. Then we can compare these two and we will get the solution.

Complete step-by-step answer:
It is given that the radius of a right circular cylinder open at both the ends is decreasing by \[25\% \] and the height of the cylinder is increased by \[25\% \].
We need to find whether the surface area of the cylinder thus formed is changed or not.
Let h be the height of the cylinder and r be the radius of the cylinder then the surface area of the cylinder is \[2\pi rh\].
After decreasing the radius by \[25\% \] it will become \[r - \dfrac{{25}}{{100}}r = \dfrac{{100 - 25}}{{100}}r = \dfrac{{75}}{{100}}r = \dfrac{3}{4}r\].
After increasing the height by \[25\% \] it will become \[h + \dfrac{{25}}{{100}}h = \dfrac{{100 + 25}}{{100}}r = \dfrac{{125}}{{100}}r = \dfrac{5}{4}r\].
Then the surface area of the cylinder is \[2\pi \dfrac{{3r}}{4}\dfrac{{5h}}{4} = \dfrac{{15}}{{16}} \times 2\pi rh\].
Since \[\dfrac{{15}}{{16}} < 1\], the surface area is decreased.
The surface area of the cylinder thus formed is decreased by
\[ = \left( {\dfrac{{2\pi rh - \dfrac{{15}}{{16}} \times 2\pi rh}}{{2\pi rh}} \times 100} \right)\% \]
Cancelling the same terms we get,
\[ = \left\{ {\left( {1 - \dfrac{{15}}{{16}}} \right) \times 100} \right\}\% \]
Simplifying we get,
\[ = \left( {\dfrac{{16 - 15}}{{16}} \times 100} \right)\% \]
Subtraction terms,
\[ = \left( {\dfrac{1}{{16}} \times 100} \right)\% \]
Hence the required solution is,
\[ = 6.25\% \]
Hence, the surface area of the cylinder thus formed is decreased by \[6.25\% \].

$\therefore $ The option (D) is the correct option.

Note:

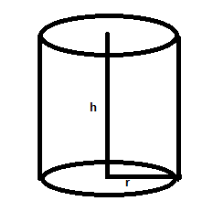
The surface area of a cylinder is \[2\pi rh\] Where r is the radius of the cylinder and h is the height of the cylinder.
Percentage formula:
Increase % = (New surface area – Original surface area)/Original surface area ×100
Decrease % = (Original surface area – new surface area)/Original surface area ×100