Question

If the radius and arc length of a sector are 17 cm and 27 cm respectively, then the perimeter is
A. 16 m
B. 61 cm
C. 32 cm
D. 80 cm

Answer 1

Hint:To solve this question, we need to know that the sector is nothing but a part of a circle which is enclosed by two radii and an arc. We also need to know that the perimeter of any shape is calculated by calculating the length of the boundary walls of the figure. We can solve this question by using these concepts.

Complete step-by-step answer:
In this question, we have been given a sector of radius 17 cm and arc length of 27 cm and we have been asked to find the perimeter of that sector. Now, we know that sector is a part of a circle that is enclosed by two radii and an arc. We can represent it by the figure as given below.

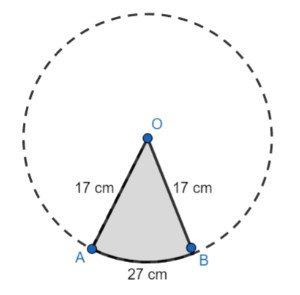
Here, we have represented OA and OB as the radius of the circle which are the part of sector and arc AB as part of the circumference of the circle which is a part of the sector. Now, we know that the perimeter of a shape is the total length of the boundary of that shape. So, we can say that perimeter of sector OAB can be calculated as,
OA + OB + Arc AB
Now, we know that the radius of the sector is 17 cm, which means that, OA = OB = 17 cm. And we have been given that the arc length is 27 cm, that is arc AB = 27 cm. So, we can write the perimeter of the sector OAB as,
17 + 17 + 27 = 61 cm.
Hence, we can say that the perimeter of the sector OAB is 61 cm. Therefore, option B is the correct answer.

Note: We can also solve this question by finding the sector angle, that is angle AOB, by using the relation $\theta =\dfrac{arc\text{ }length}{radius}$ and then to find the perimeter, we can apply the formula, perimeter of sector = $\theta \times radius+2\left( radius \right)$. But as we can see that $\theta \times radius=arc\text{ }length$, so it will indirectly reach the same stage that we reach directly via the conventional method. So, it is better to use the conventional method, if we have all the desired values.