Question

If the pulley is massless and moves with an upward acceleration \[{a_0}\], find the acceleration of \[{m_1}\] and \[{m_2}\] w.r.t. the elevator.

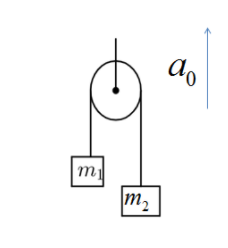
Answer 1

Hint We will begin by making the free body diagrams of the masses. Then we will write the force equations for both the masses and then we will solve them to find the acceleration of \[{m_1}\] and \[{m_2}\] w.r.t. the elevator.

Complete step by step answer
We will solve this question from a non-inertial frame of reference, i.e. we will observe the movement of both \[{m_1}\] and \[{m_2}\] by sitting on the pulley. Here, a downward pseudo force will be generated on both the masses.
We will consider, \[{m_1} < {m_2}\].

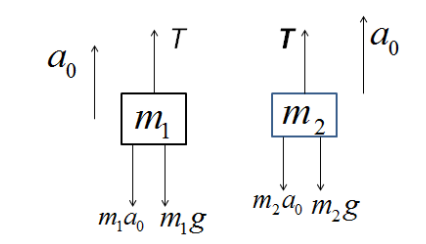
And therefore, the force equations for the movement of \[{m_1}\] and \[{m_2}\] are:
 \[T - {m_1}g - {m_1}{a_0} = {m_1}a\] …………………………………………………. (i)
 \[{m_2}g + {m_2}{a_0} - T = {m_2}a\] ………………………………………………. (ii)
Now, we will add Eq., (i.) and (ii.) we get,
 \[{m_2}(g + {a_0}) - {m_1}(g + {a_0}) = a({m_1} + {m_2})\]
 \[ \Rightarrow (g + {a_0})({m_2} - {m_1}) = a({m_1} + {m_2})\]
 \[ \Rightarrow a = \left[ {\dfrac{{({m_2} - {m_1})}}{{({m_1} + {m_2})}}} \right](g + {a_0})\]

This is the acceleration of masses \[{m_1}\] and \[{m_2}\].

Note: There is another method to solve this kind of question. We can solve this question by considering the situation of the ground frame.
In that case the force equations will have two new variables for acceleration of both the masses. This acceleration will be a sum of the acceleration of the pulley and the acceleration of the respective masses. Then we will solve the equations as usual to get the acceleration.