Question

If the position vectors of the vertices A, B and C of a $\Delta ABC$ are respectively $4\widehat{i}+7\widehat{j}+8\widehat{k}$, $2\widehat{i}+3\widehat{j}+4\widehat{k}$ and $2\widehat{i}+5\widehat{j}+7\widehat{k}$, then the position vector of the point, where the bisector of $\angle A$ meets BC is :
A. $\dfrac{1}{2}\left( 4\widehat{i}+8\widehat{j}+11\widehat{k} \right)$
B. $\dfrac{1}{3}\left( 6\widehat{i}+13\widehat{j}+18\widehat{k} \right)$
C. $\dfrac{1}{4}\left( 8\widehat{i}+14\widehat{j}+9\widehat{k} \right)$
D. $\dfrac{1}{3}\left( 6\widehat{i}+11\widehat{j}+15\widehat{k} \right)$

Answer 1

Hint: First, you need to draw the diagram and mention the given information in the diagram. Find the vectors for $\overrightarrow{AB}$ and $\overrightarrow{AC}$ and also find their magnitudes. Now, use the section formula of internal division method, $\overset{\to }{\mathop{r}}\,=\dfrac{m\overset{\to }{\mathop{b}}\,+n\overset{\to }{\mathop{a}}\,}{m+n}$, substitute the obtained values and get the result.

Complete step-by-step solution:
Let us first draw the $\Delta ABC$ denoting the vectors A as $4\widehat{i}+7\widehat{j}+8\widehat{k}$, B as $2\widehat{i}+3\widehat{j}+4\widehat{k}$ and C as $2\widehat{i}+5\widehat{j}+7\widehat{k}$ and a bisector of $\angle A$ which meets the side BC at a point D.

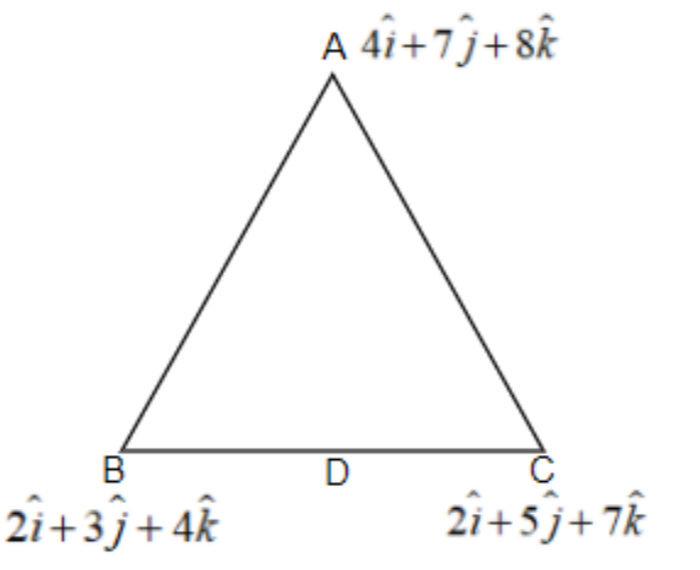
Since AD bisects the angle $\angle A$ and divides BC in the ratio AB : BC. First, let us find the vectors $\overrightarrow{AB}$ and $\overrightarrow{AC}$,
$\begin{align}
  & \overrightarrow{AB}=\left( 2\widehat{i}+3\widehat{j}+4\widehat{k} \right)-\left( 4\widehat{i}+7\widehat{j}+8\widehat{k} \right) \\
 & \Rightarrow \overrightarrow{AB}=\left( 2\widehat{i}+3\widehat{j}+4\widehat{k} \right)-4\widehat{i}-7\widehat{j}-8\widehat{k} \\
 & \Rightarrow \overrightarrow{AB}=-2\widehat{i}-4\widehat{j}-4\widehat{k} \\
\end{align}$
Similarly, let us find the vector $\overrightarrow{AC}$,
$\begin{align}
  & \overrightarrow{AC}=\left( 2\widehat{i}+5\widehat{j}+7\widehat{k} \right)-\left( 4\widehat{i}+7\widehat{j}+8\widehat{k} \right) \\
 & \Rightarrow \overrightarrow{AC}=2\widehat{i}+5\widehat{j}+7\widehat{k}-4\widehat{i}-7\widehat{j}-8\widehat{k} \\
 & \Rightarrow \overrightarrow{AC}=-2\widehat{i}-2\widehat{j}-\widehat{k} \\
\end{align}$
Now, let us find the magnitude of the vectors $\overrightarrow{AB}$ and $\overrightarrow{AC}$,
$\begin{align}
  & \left| \overrightarrow{AB} \right|=\sqrt{{{\left( -2 \right)}^{2}}+{{\left( -4 \right)}^{2}}+{{\left( -4 \right)}^{2}}} \\
 & \Rightarrow \left| \overrightarrow{AB} \right|=\sqrt{4+16+16} \\
 & \Rightarrow \left| \overrightarrow{AB} \right|=\sqrt{36} \\
 & \Rightarrow \left| \overrightarrow{AB} \right|=6 \\
\end{align}$
Similarly, the magnitude of vector $\overrightarrow{AC}$ will be,
$\begin{align}
  & \left| \overrightarrow{AC} \right|=\sqrt{{{\left( -2 \right)}^{2}}+{{\left( -2 \right)}^{2}}+{{\left( -1 \right)}^{2}}} \\
 & \Rightarrow \left| \overrightarrow{AC} \right|=\sqrt{4+4+1} \\
 & \Rightarrow \left| \overrightarrow{AC} \right|=\sqrt{9} \\
 & \Rightarrow \left| \overrightarrow{AC} \right|=3 \\
\end{align}$
By using section formula of internal division method, we know,
$\overset{\to }{\mathop{r}}\,=\dfrac{m\overset{\to }{\mathop{b}}\,+n\overset{\to }{\mathop{a}}\,}{m+n}\ldots \ldots \ldots \left( i \right)$
Here, according to the above expression, we have,
$\begin{align}
  & m=\left| \overleftrightarrow{AB} \right|=6 \\
 & n=\left| \overleftrightarrow{AC} \right|=3 \\
\end{align}$
Let us consider $\overset{\to }{\mathop{a}}\,$ as $\overset{\to }{\mathop{B}}\,$ and $\overset{\to }{\mathop{b}}\,$ as $\overset{\to }{\mathop{C}}\,$ and $\overset{\to }{\mathop{r}}\,$ as $\overset{\to }{\mathop{D}}\,$. Therefore, we get,
$\overset{\to }{\mathop{a}}\,=2\widehat{i}+3\widehat{j}+4\widehat{k}$ and $\overset{\to }{\mathop{b}}\,=2\widehat{i}+5\widehat{j}+7\widehat{k}$
Now, when we substitute the values of m and n, the vectors $\overset{\to }{\mathop{a}}\,$ and $\overset{\to }{\mathop{b}}\,$ in the equation (i), we will get the position vector of D, which is,
$\begin{align}
  & \overset{\to }{\mathop{D}}\,=\dfrac{6\left( 2\widehat{i}+5\widehat{j}+7\widehat{k} \right)+3\left( 2\widehat{i}+3\widehat{j}+4\widehat{k} \right)}{6+3} \\
 & \Rightarrow \overset{\to }{\mathop{D}}\,=\dfrac{3\left[ 2\left( 2\widehat{i}+5\widehat{j}+7\widehat{k} \right)+\left( 2\widehat{i}+3\widehat{j}+4\widehat{k} \right) \right]}{9} \\
 & \Rightarrow \overset{\to }{\mathop{D}}\,=\dfrac{1}{3}\left[ 4\widehat{i}+10\widehat{j}+14\widehat{k}+2\widehat{i}+3\widehat{j}+4\widehat{k} \right] \\
 & \Rightarrow \overset{\to }{\mathop{D}}\,=\dfrac{1}{3}\left[ 6\widehat{i}+13\widehat{j}+18\widehat{k} \right] \\
\end{align}$
Therefore, the position vector of D is $\dfrac{1}{3}\left[ 6\widehat{i}+13\widehat{j}+18\widehat{k} \right]$.
Hence, the correct option is option B.

Note: In this question, always draw the diagram which makes it easy to understand the question. You also need to know, how to get the position vectors and how to find the magnitude of the vectors. The vector in the form of I, j, k represents the position of a vector in three-dimensional graph y x, y, z respectively.