Question

If the point $\left( {1,4} \right)$ lies inside the circle ${x^2} + {y^2} - 6x - 10y + p = 0$ and the circle does not touch or intersect the coordinate axes, then the set of all possible values of p is the interval:
A) $\left( {0,25} \right)$
B) $\left( {25,39} \right)$
C) $\left( {9,25} \right)$
D) $\left( {25,29} \right)$

Answer 1

Hint: A circle is a collection of points from a fixed point at a fixed distance. The fixed point is called a center and the fixed distance is the radius of the circle.
Equation of the circle with center \[\left( {h,k} \right)\] and radius $r{\text{ }}units$ is given by:
\[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\]
If the point lies outside the circle then the radius of the circle will be less than the length of the point from the center of the circle. Try to use this while satisfying the given point in the equation of the given circle.
The given equation of the circle is the expanded form of the standard equation of the circle.
On expanding using ${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$ , we get
\[
  {x^2} + {h^2} - 2hx + {y^2} + {k^2} - 2ky - {r^2} = 0 \\
   \Rightarrow {x^2} + {y^2} - 2hx - 2ky + {h^2} + {k^2} - {r^2} = 0 \\
 \]
The equation of the circle is also given in this form, you can identify that the given equation is the equation of the circle if the equation has a ${x^2}$ term, ${y^2}$ term, x term, $y$ term, and some constant.

Complete step-by-step answer:
Step 1: Find the condition for a point lying inside the circle.
Given points in the question lie inside the circle, let us understand what it means.

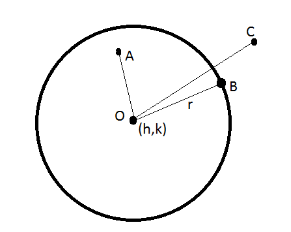
Let point $A\left( {{x_1},{y_1}} \right)$ lie inside the circle with center \[O\left( {h,k} \right)\] and radius r.
Then, the length $AO < OB$
$\because AO < r$
Length AO using the distance formula i.e.
Distance formula for two points in the cartesian plane.
Let coordinates of a point A is $\left( {{x_1},{y_1}} \right)$ and a point B is $\left( {{x_2},{y_2}} \right)$ .
The distance between points A and B or the length AB is given by
$AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $

\[ \Rightarrow \sqrt {{{\left( {h - {x_1}} \right)}^2} + {{\left( {k - {y_1}} \right)}^2}} < r\]
Squaring both sides.
\[{\left( {h - {x_1}} \right)^2} + {\left( {k - {y_1}} \right)^2} < {r^2}\]
On expansion using ${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$ , we get
$ \Rightarrow {x_1}^2 + {y_1}^2 - 2h{x_1} - 2k{y_1} + {h^2} + {k^2} < {r^2}$
Take the ${r^2}$ to the left side of the equation, then the whole equation of the circle will be less than 0.
$ \Rightarrow {x_1}^2 + {y_1}^2 - 2h{x_1} - 2k{y_1} + {h^2} + {k^2} - {r^2} < 0$
The expression ${x_1}^2 + {y_1}^2 - 2h{x_1} - 2k{y_1} + {h^2} + {k^2} - {r^2}$ , we also get after putting the point A in the equation of the circle.
$ \Rightarrow {x_1}^2 + {y_1}^2 - 2h{x_1} - 2k{y_1} + {h^2} + {k^2} - {r^2} < 0$ , hence we use this condition for the point $A\left( {{x_1},{y_1}} \right)$lying inside the circle.
Step 2: Satisfy the condition for a point lying inside the circle.
The given equation the circle ${x^2} + {y^2} - 6x - 10y + p = 0$
Let the point $A\left( {1,4} \right)$ lie inside the circle.

Hence, put $A\left( {1,4} \right)$ in the equation of the circle, the equation will be less than 0 according to the steps done in step 1. Substitute x with 1 and y with 4.
 ${x^2} + {y^2} - 6x - 10y + p < 0$
\[{1^2} + {4^2} - 6\left( 1 \right) - 10\left( 4 \right) + p < 0\]
Solve further and find the interval of p.
\[
   \Rightarrow 1 + 16 - 6 - 40 + p < 0 \\
   \Rightarrow + 17 - 46 + p < 0 \\
   \Rightarrow - 29 + p < 0 \\
 \]
\[ \Rightarrow p < 29\] …… (1)
Step 3: Use the condition that the circle does not touch or intersect any coordinate axes.
Given the circle does not intersect the x-axis, this means $y \ne 0$
This means for y = 0, in the given equation of the circle,
\[{x^2} + {\left( 0 \right)^2} - 6x - 10\left( 0 \right) + p = 0\]
${x^2} - 6x + p = 0$ , the solution to this quadratic equation does not exist because the circle does not intersect the x-axis.
For discriminant < 0, the solution to the quadratic equation does not exist.
We know for the quadratic equation $a{x^2} + bx + c = 0$, discriminant, \[D = {b^2} - 4ac\] , where a, b, and c are constant coefficients.
On comparing with the standard quadratic equation:
$a = 1;{\text{ }}b = - 6;{\text{ }}c = p$
Discriminant, $D < 0$
$
   \Rightarrow {\left( { - 6} \right)^2} - 4\left( 1 \right)\left( p \right) < 0 \\
   \Rightarrow 36 - 4p < 0 \\
   \Rightarrow - 4p < - 36 \\
 $
On multiplying both sides by the minus sign, the sign of inequality reverses.
$ \Rightarrow 4p > 36$
$\because p > 9$ …… (2)
Given the circle does not intersect the x-axis, this means $x \ne 0$
This means for x = 0, in the given equation of the circle,
\[{\left( 0 \right)^2} + {y^2} - 6\left( 0 \right) - 10y + p = 0\]
${y^2} - 10y + p = 0$ , the solution to this quadratic equation does not exist.
For discriminant < 0, the solution to the quadratic equation does not exist because the circle does not intersect the y-axis.
We know for the quadratic equation $a{x^2} + bx + c = 0$, discriminant, \[D = {b^2} - 4ac\] , where a, b, and c are constant coefficients.
On comparing with the standard quadratic equation:
$a = 1;{\text{ }}b = - 10;{\text{ }}c = p$
Discriminant, $D < 0$
$
   \Rightarrow {\left( { - 10} \right)^2} - 4\left( 1 \right)\left( p \right) < 0 \\
   \Rightarrow 100 - 4p < 0 \\
   \Rightarrow - 4p < - 100 \\
 $
On multiplying both sides by the minus sign, the sign of inequality reverses.
$ \Rightarrow 4p > 100$
$\because p > 25$ …… (3)
Step 4: Find the interval of the P
The interval of P should satisfy all the inequality obtained in equation (1), (2), and (3).
The interval of P can be found out using a graphical method.

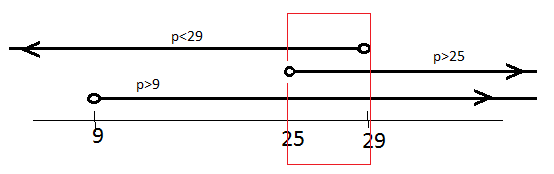
Thus the common interval of P satisfying all the inequality obtained in equation (1), (2), and (3).
$p \in \left( {25,29} \right)$
Final answer: In the interval $p \in \left( {25,29} \right)$ for which the point $\left( {1,4} \right)$ lies inside the given circle, thus the correct option is (D).

Note: Let us derive the condition for the point lying outside the circle. This will be helpful in future questions.

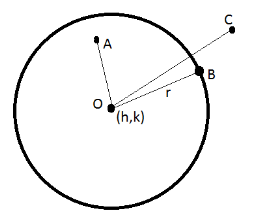
Let the point $C\left( {{x_2},{y_2}} \right)$ lies outside the circle with center O and radius r.
Then, the length $CO < OB$ . This implies that the length CO is less than the radius of the circle.
$\because CO < r$
Thus the equation of the circle satisfying point $C\left( {{x_2},{y_2}} \right)$ will be greater than 0.
$ \Rightarrow {x_2}^2 + {y_2}^2 - 2h{x_2} - 2k{y_2} + {h^2} + {k^2} - {r^2} > 0$ . It is the condition for the point $\left( {{x_2},{y_2}} \right)$ lying outside the circle.
Now, let us derive the condition for the point lying on the circle. This will also be helpful in future questions.
Let the point $B\left( {{x_3},{y_3}} \right)$ lie on the circle with center O and radius r.
Then, the length $BO = OB$. This implies that the length BO is equal to the radius of the circle.
$\because BO = r$
Thus the equation of the circle satisfying point $B\left( {{x_3},{y_3}} \right)$ will be equal to 0.
$ \Rightarrow {x_3}^2 + {y_3}^2 - 2h{x_3} - 2k{y_3} + {h^2} + {k^2} - {r^2} > 0$. It is the condition for the point $\left( {{x_3},{y_3}} \right)$ lying on the circle.
Remember if we are taking the distance in a 3-dimensional coordinate system use the Distance formula for two points in the 3-dimensional cartesian plane. I.e.
Let coordinates of a point A is $\left( {{x_1},{y_1},{z_1}} \right)$ and a point B is $\left( {{x_2},{y_2},{z_2}} \right)$ .
The distance between points A and B or the length AB is given by
$AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} $