Question

If the parallel sides of the trapezium field are 80m and 20m. These sides meet the third side at the right angle. The length of the fourth side is 90m. If it costs Rs. 5 to plow per ${{m}^{2}}$ of the field, find the total cost of plowing the field.

Answer 1

Hint: To find the cost of plowing the trapezium fields we are required to first find the area of the trapezium field. Area of the trapezium is given by: $\dfrac{1}{2}\times \left( \text{Sum of parallel sides} \right)\times \text{height}$. We already have the parallel sides, we have to first find the height and then we will calculate the area to find the cost of plowing.

Complete step-by-step solution
We know that two sides of the trapezium are always parallel. And, the parallel sides of the trapezium meet the third side at the right angle. So, the third side is perpendicular to both the parallel side of the triangle.
Let us assume that ABDC is the trapezium field in which AB is parallel to CD and let AC be the third side which is perpendicular to AB as well as CD.

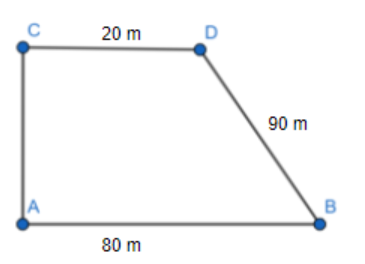
So, from the question, we know that length of the parallel sides of the trapezium field is 80m and 20m.
So, $AB = 80m$ and $CD = 20m$
And, length of the fourth side, that is BD is equal to 90m.
Now, let us draw a line parallel to AC and perpendicular to line AB from point D.

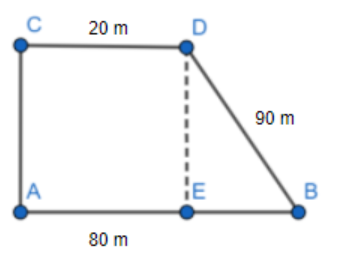
Now, we know that DE is perpendicular to line AB so $\Delta DEB$ is a right angle triangle and DE is parallel and equal to AC and similarly, AE is equal and parallel to CD.
i.e. $DE = AC$ and $AE = CD $…………….(1)
Now, from the figure we can see that:
$AB = AE + EB$
$\Rightarrow EB = AB - AE $
So, $EB = AB – CD$ (from (1)) …………………..(2)
Now, we know that $\Delta DEB$ is a right angle triangle, so from pythagoras theorem, we can say that:
$D{{E}^{2}}+E{{B}^{2}}=D{{B}^{2}}$
Now, from (1) and (2) equation, we will get:
${{\left( AC \right)}^{2}}+{{\left( AB-CD \right)}^{2}}=D{{B}^{2}}$
And, we that know, AB = 80m, CD = 20m and BD = 90m
Putting the value in above equation, we will get:
$\Rightarrow {{\left( AC \right)}^{2}}+{{\left( 80-20 \right)}^{2}}={{90}^{2}}$
$\Rightarrow A{{C}^{2}}=\left( 8100-3600 \right){{m}^{2}}$
$\Rightarrow AC=\sqrt{4500}m$
$\therefore AC=67.082m$
We know that area of the trapezium is given by $\dfrac{1}{2}\times \left( \text{Sum of parallel sides} \right)\times \text{height}$
So, area of the trapezium ABDC = $\dfrac{1}{2}\times \left( AB+CD \right)\times AC$
$=\dfrac{1}{2}\left( 80+20 \right)\times 67.082{{m}^{2}}$
So, area of the trapezium field = \[\text{3,354}\text{.1}{{\text{m}}^{2}}\]
We know that cost of plough per ${{m}^{2}}$is Rs. 5
So, cost of ploughing \[\text{3,354}\text{.1}{{\text{m}}^{2}}\] = \[\text{Rs}\text{.3,354}\text{.1}\times \text{5}\] = Rs 16,770.5
This is our required solution.

Note: We can also calculate the area of the trapezium ABDC just by finding the area of triangle $\Delta DEB$ and the rectangle AEDC separately and then by adding both areas we will get the area of trapezium. We will multiply the height and base and then divide it by 2 to get the area of the triangle and multiplying the length and breadth, we will get the area of the rectangle.