Question

If the middle points of the sides \[BC,CA\] AND \[AB\] of the triangle \[ABC\] be\[(1,3),(5,7)\] and \[( - 5,7)\] respectively then the equation of the side \[AB\] is
1. \[x - y - 2 = 0\]
2. \[x - y + 12 = 0\]
3. \[x + y - 12 = 0\]
4. None of these

Answer 1

Hint: In the question, we are given the midpoints of the sides of a triangle and we are asked to find the equation of a line using the given information. In order to get this, we need to find the slope of the line parallel to the required line as we know that the slope of two parallel lines is the same. After finding the slope we will use the slope intercept form to find the required equation of line. We will use the midpoint theorem of a triangle that states that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and its length is equal to half of the third side.

Complete step-by-step solution:

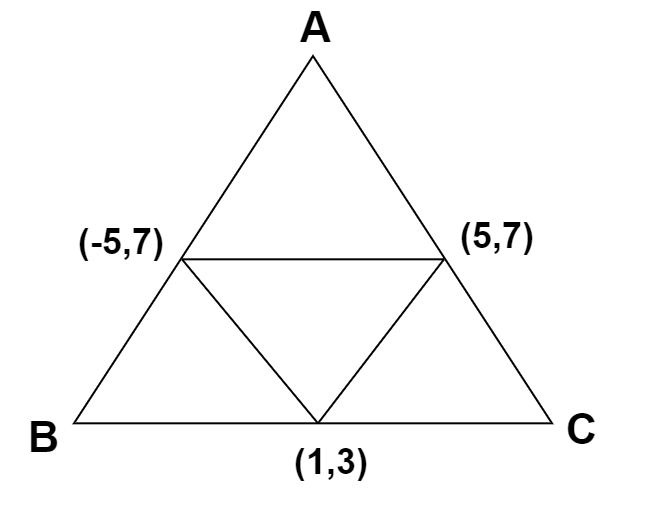
The line AB will be parallel to the line joining midpoints of AC and BC using the midpoint theorem of a triangle that states that the line segment joining the midpoints of two sides is parallel to the third side and the length is equal to half of that of the third side.
Since the slope of two parallel lines is the same.
Therefore slope of line AB \[ = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \dfrac{{7 - 3}}{{5 - 1}} = 1\]
Now, using the slope point form of a line and putting in all the known values, we get the equation of line AB as,
\[y - {y_1} = m(x -{x_1 })\]
\[\Rightarrow y - 7 = 1(x + 5)\]
\[\Rightarrow x - y + 12 = 0\]
Hence we get the required equation of the side.
Therefore option (2) is the correct answer.

Note: We should always make a diagram in such questions using the information given in the question so as to understand it completely. Keep in mind that the slope of a straight line between two points say \[\left( {{x_1},{y_1}} \right)\]and \[\left( {{x_2},{y_2}} \right)\] can be easily determined by finding the difference between the coordinates of the points. The slope is usually represented by the letter ‘m’. The slope point form of a straight line is $\dfrac{{y - {y_1}}}{{x - {x_1}}} = m$ where m denotes the slope of line and $\left( {{x_1},{y_1}} \right)$ denotes the coordinates of the point lying on the line segment.