Question

If the man continues pushing the block by force \[F\], its acceleration would be

A. \[\dfrac{g}{6}\]
B. \[\dfrac{g}{4}\]
C. \[\dfrac{g}{2}\]
D. \[g\]

Answer 1

Hint: A block is being pushed by a force \[F\]. The acceleration will depend on the normal component \[N\], the angle of inclination \[\theta \] and the frictional force \[f\] between the block and the slider. Drawing a free body diagram by resolving all the components of friction and force applied will help in finding the acceleration of the object.

Formula Used:
The normal component of the force is given as: \[N = mg\cos \theta \]
where, \[N\] is the normal component of the force, \[m\] is the mass of the object and \[g\] is acceleration due to gravity
\[\theta = {30^ \circ }\] is the angle of inclination
The frictional force \[f\] is given as: \[f = \mu N\]
The coefficient of friction \[\mu \] is given as: \[\mu = \tan \theta \], where \[\theta \] is the angle of inclination.

Complete step by step solution:

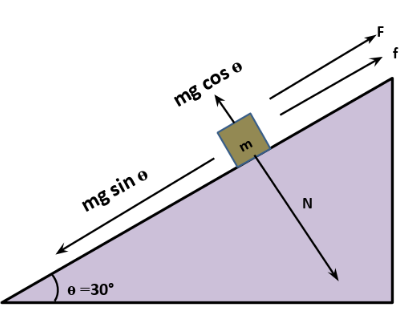
The normal component is directed upwards as shown in the figure. This normal reaction on the horizontal surface is equal to the weight of the object. But on an inclined plane, it is given by
\[N = mg\cos \theta = mg\cos {30^ \circ }\] \[ \to (1)\]
\[\theta = {30^ \circ }\] is the angle of inclination
The frictional force \[f\] is proportional to its normal force \[N\].
\[f \propto N\] or \[f = \mu N\] \[ \to (2)\]
The coefficient of friction \[\mu \]can also be written as
\[\mu = \tan \theta = \tan {30^ \circ }\] \[ \to (3)\]
Substituting equation (1) and (3) in equation (2)
\[f = - \mu N \\
\Rightarrow f = \left[ { - \tan \theta \times mg\cos \theta } \right] \\
\Rightarrow f = \left[ { - \tan {{30}^ \circ } \times mg\cos {{30}^ \circ }} \right]\] \[ \to (4)\]

On the inclined plane, the pull due to gravity is \[mg\sin \theta = mg\sin {30^ \circ }\]. The force by which the man continues to push the block is given by\[F = ma\]where \[a\] is the acceleration. The force \[F\] is directed in a direction opposite to \[mg\sin \theta \]. (Refer the diagram)
Resolving the components of force
\[
mg\sin \theta = F + f \\
\Rightarrow mg\sin {30^ \circ } = ma + \left[ { - \tan {{30}^ \circ } \times mg\cos {{30}^ \circ }} \right] \\
\Rightarrow g\sin {30^ \circ } = a - (\tan {30^ \circ } \times m\cos {30^ \circ }) \\
\Rightarrow a = g\sin {30^ \circ } + \tan {30^ \circ } \times m\cos {30^ \circ } \\
\Rightarrow a = \left( {g \times \dfrac{1}{2}} \right) + \left( {\dfrac{1}{{\sqrt 3 }} \times g \times \dfrac{{\sqrt 3 }}{2}} \right) \\
\Rightarrow a = \dfrac{1}{2}g + \dfrac{1}{2}g \\
\therefore a = g \]
Thus, the acceleration is \[g\].

Hence, option D is the correct answer.

Note: When the plane is tilted at \[\theta \], the object will slide steadily in halting fashion. At one place it may stop and at other places it may move with acceleration. This behaviour indicates that the coefficient of friction \[\mu \]is just a rough constant and varies from place to place along the plane. Such variations are caused by different degrees of smoothness and hardness of the plane.