Question

If the line $\dfrac{x}{a} + \dfrac{y}{b} = \sqrt 2 $ touches the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$, then the eccentric angle theta of point of contact is equal to-
$
  {\text{A}}{\text{. }}{{\text{0}}^0} \\
  {\text{B}}{\text{. 9}}{{\text{0}}^0} \\
  {\text{C}}{\text{. 4}}{{\text{5}}^0} \\
  {\text{D}}{\text{. 6}}{{\text{0}}^0} \\
$

Answer 1

Hint: Assume parametric points and find the tangent through that point using T=0. Compare the coefficients from the tangent equation already given. Then find the eccentric angle.

Complete step-by-step answer:
The given equation of ellipse is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$. The equation of one of the tangents is given as$\dfrac{x}{a} + \dfrac{y}{b} = \sqrt 2 $.
The length of semi-major axes is given as a and length of semi-minor axes is given as b.
The eccentric angle of a point on an ellipse with semi-major axes of length a and semi-minor axes of length b is the angle of parametrization.

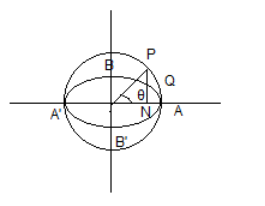
 Θ is the eccentric angle here.
Let us assume a point on the ellipse (x1,y1)
The equation of tangent at this point can be written as T=0 and this can be written as:
\[\dfrac{{x{x_1}}}{{{a^2}}} + {\text{ }}\dfrac{{y{y_1}}}{{{b^2}}}-{\text{ }}1{\text{ }} = {\text{ }}0\]
We can take (x1,y1) to be parametric coordinates and hence they will be substituted as:
\[\begin{array}{*{20}{l}}
  {{x_1}{\text{ }} = {\text{ }}a\cos \left( \phi \right)} \\
  {{y_1}{\text{ }} = {\text{ }}b\sin \left( \phi \right)}
\end{array}\]
Now substitute the values of x1 and y1 in the equation T=0, the equation of tangent in parametric form can be written as:
\[\dfrac{{x\cos \phi }}{a} + {\text{ }}\dfrac{{y\sin \phi }}{b}-{\text{ }}1{\text{ }} = {\text{ }}0\]
The equation of one of its tangents is given in the question and so now we will compare both these equations because they are the same.
Now by comparing both the equations, we get,
\[\dfrac{{x\cos \phi }}{a} + {\text{ }}\dfrac{{y\sin \phi }}{b}-{\text{ }}1{\text{ }} = {\text{ }}0\]
$\dfrac{x}{a} + \dfrac{y}{b} = \sqrt 2 $.
By comparing these two equations, we get,
\[\begin{array}{*{20}{l}}
  {\cos \left( \phi \right){\text{ }} = {\text{ }}\dfrac{1}{{\sqrt 2 }}} \\
  {\sin \left( \phi \right){\text{ }} = {\text{ }}\dfrac{1}{{\sqrt 2 }}}
\end{array}\]
So,\[\phi {\text{ }} = {\text{ }}{45^0}\]
Therefore, the eccentric angle is 45 degrees.
The correct option is C.

Note: The parametric points are in terms of the eccentric angle, this is why the polar form of parametric points was assumed and not the Cartesian format.