Question

If the line $4x-3y-8=0$ cuts the parabola ${{x}^{2}}+y-4=0$ at A and B, and PA.PB is equal to $\dfrac{k}{8}$ (where P=(0,2)), then find the value of k.

Answer 1

Hint: In this question, we are given the equation of a parabola and a straight line and are asked to find the distance of the points of intersection of the line and a fixed point P. Therefore, as the point of intersection of the line should lie on both the parabola and the line, we can simultaneously solve the equation of the line and the parabola and then find the distance from the points of intersection to the given point P(0, 2) using the formula for distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ $\left( d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}} \right)$ . We can then equate this value to $\dfrac{k}{8}$ and solve the resulting value of k to obtain the required answer.

Complete step-by-step solution -
The given equation of the parabola is ${{x}^{2}}+y-4=0......................................(1.1)$
And the equation of the straight line is
$\begin{align}
  & 4x-3y-8=0 \\
 & \Rightarrow 3y=4x-8 \\
 & \Rightarrow y=\dfrac{4x-8}{3}............................(1.2) \\
\end{align}$
The parabola and the line are as shown in the following figure

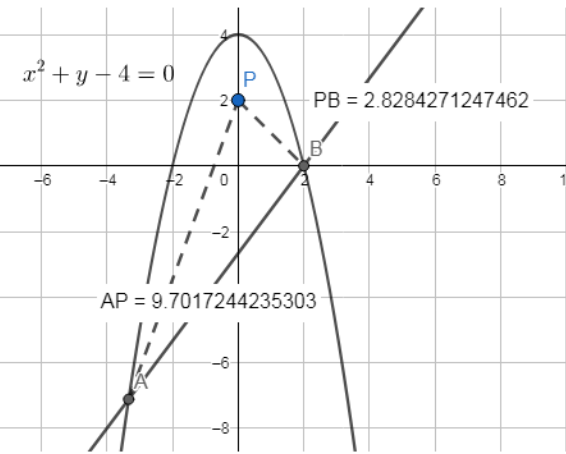
As the point of intersection should lie on both the straight line and the parabola, it should satisfy both equations for the line and the parabola. Thus, it should satisfy both (1.1) and (1.2). Therefore, putting the value of y from (1.2) in (1.1), we obtain
$\begin{align}
  & {{x}^{2}}+\dfrac{4x-8}{3}-4=0 \\
 & \Rightarrow 3{{x}^{2}}+4x-8-3\times 4=0 \\
 & \Rightarrow 3{{x}^{2}}+4x-20=0..................(1.3) \\
\end{align}$
Now, we know that the formula for the solutions of a quadratic equation $a{{x}^{2}}+bx+c=0$ is given by
$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}....................(1.4)$
Therefore, using equation (1.4) in equation (1.3) with a=3, b=4 and c=-20, we obtain
$\begin{align}
  & x=\dfrac{-4\pm \sqrt{{{4}^{2}}-4\times 3\times -20}}{2\times 3}=\dfrac{-4\pm \sqrt{256}}{6}=\dfrac{-4\pm 16}{6} \\
 & \Rightarrow x=\dfrac{-4-16}{6}=\dfrac{-10}{3}\text{ or }x=\dfrac{-4+16}{6}=\dfrac{+12}{6}=2 \\
\end{align}$
Now, we can use these values of x in (1.2) to find the corresponding values of y as
If $x=\dfrac{-10}{3}$ , then $y=\dfrac{4x-8}{3}=\dfrac{4\times \dfrac{-10}{3}-8}{3}=\dfrac{-64}{9}$
If $x=2$ , then $y=\dfrac{4x-8}{3}=\dfrac{4\times 2-8}{3}=\dfrac{8-8}{3}=0$
Therefore, the points of intersection are $A=\left( \dfrac{-10}{3},\dfrac{-64}{9} \right)$ and $B=\left( 2,0 \right)$ ………………………(1.5)
We know that the formula for finding the distance between 2 points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by$d=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}..........................(1.6)$
Therefore, from (1.5) and (1.6), the distance between the point P(0,2) and A and B is given by
\[\begin{align}
  & PA=\sqrt{{{\left( \dfrac{-10}{3}-0 \right)}^{2}}+\left( \dfrac{-64}{9}-2 \right)} \\
 & =\sqrt{{{\left( \dfrac{-10}{3} \right)}^{2}}+{{\left( \dfrac{-82}{9} \right)}^{2}}} \\
 & =\sqrt{\left( \dfrac{100}{9} \right)+\left( \dfrac{6724}{81} \right)}=\sqrt{\dfrac{900+6724}{81}}=\sqrt{\dfrac{7624}{81}} \\
 & =\dfrac{\sqrt{7624}}{9}...........................(1.7) \\
\end{align}\]
and
$\begin{align}
  & PB=\sqrt{{{\left( 2-0 \right)}^{2}}+{{\left( 0-2 \right)}^{2}}}=\sqrt{4+4} \\
 & =2\sqrt{2}.....................(1.8) \\
\end{align}$
Therefore, multiplying PA and PB, we obtain
$\begin{align}
  & PA.PB=\sqrt{\dfrac{7624}{81}}\times 2\sqrt{2}=2\sqrt{\dfrac{7624\times 2}{81}} \\
 & =2\times \dfrac{\sqrt{15248}}{9}......................(1.9) \\
\end{align}$
However, it is given that the $PA.PB=\dfrac{k}{8}$ , therefore equating it to (1.9), we obtain
$\begin{align}
  & \dfrac{k}{8}=\dfrac{2}{9}\times \sqrt{15248} \\
 & \Rightarrow k=8\times \dfrac{2}{9}\times \sqrt{15248}\approx 219.52 \\
\end{align}$
Thus the required value of k is 219.52.

Note: We should note that in equation (1.5), we could have also chosen the points A and B as $A=\left( 2,0 \right)$ and $B=\left( \dfrac{-10}{3},\dfrac{-64}{9} \right)$ as we are just given that A and b are the points of intersection. However, the final answer would remain unchanged as the value of k depends on the product of PA and PB and the product (PA.PB) would remain the same if we interchange the points A and B.