
If the letters of the word QUESTION are arranged at random, the probability that there will be exactly 2 letters in between Q and U is
a) $\dfrac{{}^{6}{{P}_{2}}}{8!}$
b) $\dfrac{{}^{6}{{P}_{2}}\times 2}{8!}$
c) $\dfrac{{}^{6}{{P}_{2}}\times 5!\times 2}{8!}$
d) $\dfrac{{}^{6}{{P}_{2}}\times 2}{8!}$
Answer
585.6k+ views
Hint: The word QUESTION has 8 letters. We need to arrange Q and U in such a way that there are only two letters in between them, i.e. $\text{Q }\!\!\_\!\!\text{ }\!\!\_\!\!\text{ U}$. So, we have to arrange 6 letters between them. Find different orientations in which the letters can be arranged. Also, find the number of orientations when Q and U are interchanged.
Complete step by step answer:
Now, use the given data to find the probability of exactly 2 letters in between Q and U.
Since total letters in word Question are 8. We have to arrange exactly two letters between Q and U. So, we need to choose 2 letters from the remaining 6 letters.
So, we have:${}^{6}{{C}_{2}}$
Next, as we can arrange the letters between Q and U in the following manner:
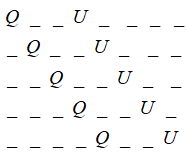
And similarly, by interchanging Q and U, we get:
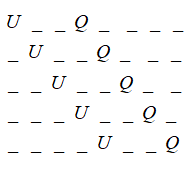
So, we can put the set of Q and U at 5 places, and could also arrange Q and U in 2 ways.
Therefore, the number of orientations is: $5!\times 2$
We need to choose exactly 2 letters between Q and U. So, the required probability is:
$=\dfrac{{}^{6}{{C}_{2}}\times 2!\times 4!}{8!}\times 5!\times 2$
Since, $C(n,r)=\dfrac{P(n,r)}{r!}$
We can write the probability as:
$=\dfrac{{}^{6}{{P}_{2}}}{8!}\times 5!\times 2$
So, the correct answer is “Option C”.
Note: While applying permutations and combinations, always be careful with the identities. Also, while finding the probability, always look for whichever orientation possible. Do not miss any orientation. And, do find the number of orientations when the letters are interchanged. Some might miss that case.
Complete step by step answer:
Now, use the given data to find the probability of exactly 2 letters in between Q and U.
Since total letters in word Question are 8. We have to arrange exactly two letters between Q and U. So, we need to choose 2 letters from the remaining 6 letters.
So, we have:${}^{6}{{C}_{2}}$
Next, as we can arrange the letters between Q and U in the following manner:
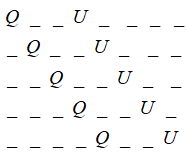
And similarly, by interchanging Q and U, we get:
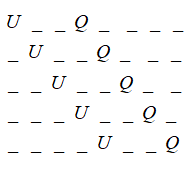
So, we can put the set of Q and U at 5 places, and could also arrange Q and U in 2 ways.
Therefore, the number of orientations is: $5!\times 2$
We need to choose exactly 2 letters between Q and U. So, the required probability is:
$=\dfrac{{}^{6}{{C}_{2}}\times 2!\times 4!}{8!}\times 5!\times 2$
Since, $C(n,r)=\dfrac{P(n,r)}{r!}$
We can write the probability as:
$=\dfrac{{}^{6}{{P}_{2}}}{8!}\times 5!\times 2$
So, the correct answer is “Option C”.
Note: While applying permutations and combinations, always be careful with the identities. Also, while finding the probability, always look for whichever orientation possible. Do not miss any orientation. And, do find the number of orientations when the letters are interchanged. Some might miss that case.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




