Question

If the lengths of parallel sides of trapezium are 8cm, 9cm and the distance between the parallel sides is 6cm, then its area is
(a). 34 sq cm
(b). 68 sq cm
(c). 51 sq cm
(d). 72 sq cm

Answer 1

Hint: Use the formula that the area of the trapezium is equal to the product of the sum of the parallel sides and the distance between them multiplied by half, i.e., $\dfrac{1}{2}\times \left( \text{sum of parallel sides} \right)\times \left( \text{distance between parallel sides} \right)$ . Just put the values in the formula to get the answer.

Complete step-by-step answer:

Let us start the solution to the above question by drawing the diagram.

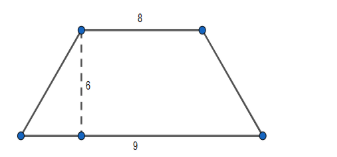
In the question, it is given that the parallel sides of the trapezium are of the lengths 8cm and 9cm. It is also given that the distance between the two parallel sides is equal to 6cm.
We know that the formula that the area of the trapezium is equal to the product of the sum of the parallel sides and the distance between them multiplied by half, i.e., $\dfrac{1}{2}\times \left( \text{sum of parallel sides} \right)\times \left( \text{distance between parallel sides} \right)$
 $=\dfrac{1}{2}\times \left( 8+9 \right)\times 6=\dfrac{1}{2}\times 17\times 6=51c{{m}^{2}}$
Therefore, we can conclude that the area of the trapezium with dimensions as given in the question is equal to 51 sq cm. Hence, the answer to the above question is option (c).

Note: Be careful in the calculation part and learn all the formulas related to different types of quadrilaterals like kite, parallelogram etc. and be sure that you don’t confuse the area of the trapezium with the formula $\dfrac{1}{2}\times \left( \text{product of diagonals} \right)$ instead of the correct formula $\dfrac{1}{2}\times \left( \text{sum of parallel sides} \right)\times \left( \text{distance between parallel sides} \right)$ . Also, learn all the formulas related to the area and perimeter of the circle.