Question

If the length of the tangent from $\left( h,k \right)$ to the circle ${{x}^{2}}+{{y}^{2}}=16$ is twice the length of the tangent from the same point to the circle ${{x}^{2}}+{{y}^{2}}+2x+2y=0,$ then
(a) ${{h}^{2}}+{{k}^{2}}+4h+4k+16=0$
(b) ${{h}^{2}}+{{k}^{2}}+3h+3k=0$
(c)$3{{h}^{2}}+3{{k}^{2}}+8h+8k+16=0$
(d) $3{{h}^{2}}+3{{k}^{2}}+4h+4k+16=0$

Answer 1

Hint: Use the standard formula for length of tangent from any point to circle and use the given condition given. Using both the conditions we will get our required solution.

Complete step by step solution:
As we have two circles
${{x}^{2}}+{{y}^{2}}=16$
${{x}^{2}}+{{y}^{2}}+2x+2y=0,$
Comparing the above equation with ${{x}^{2}}+{{y}^{2}}+2gx+2fy+C=0$ (Standard equation of circle)
Centre of circle $=\left( -g,-f \right)$
Radius $=\sqrt{{{g}^{2}}+{{f}^{2}}-C}$
Hence, centre of the first circle $=\left( 0,0 \right)$
Radius=$\sqrt{16}=4$
Centre of the second circle $=\left( -1,-1 \right)$
Radius=$\sqrt{{{1}^{2}}+{{1}^{2}}-0}=\sqrt{2}$
We have a point $\left(h,k \right)$ from where tangent to first circle and second circle are drawn as shown follows:

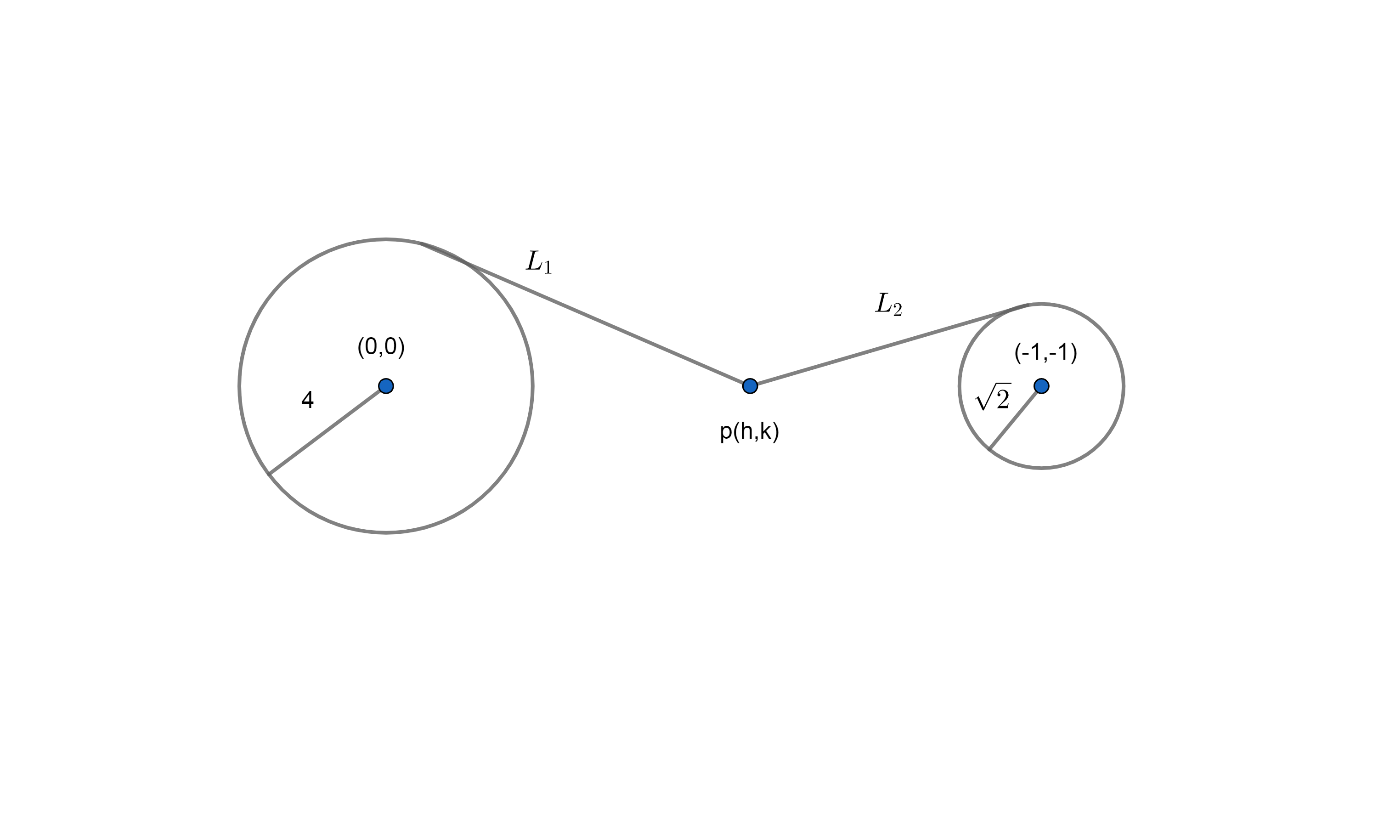
${{x}^{2}}+{{y}^{2}}=16{{x}^{2}}+{{y}^{2}}+2x+2y=0,$

${{L}_{1}}=$ length of tangent from $\left( h,k \right)$ to first circle
${{L}_{2}}=$ length of tangent from $\left( h,k \right)$ to second circle
Now, let us look at the length of the tangent from a point $\left(h,k \right)$ to a standard equation of circle.

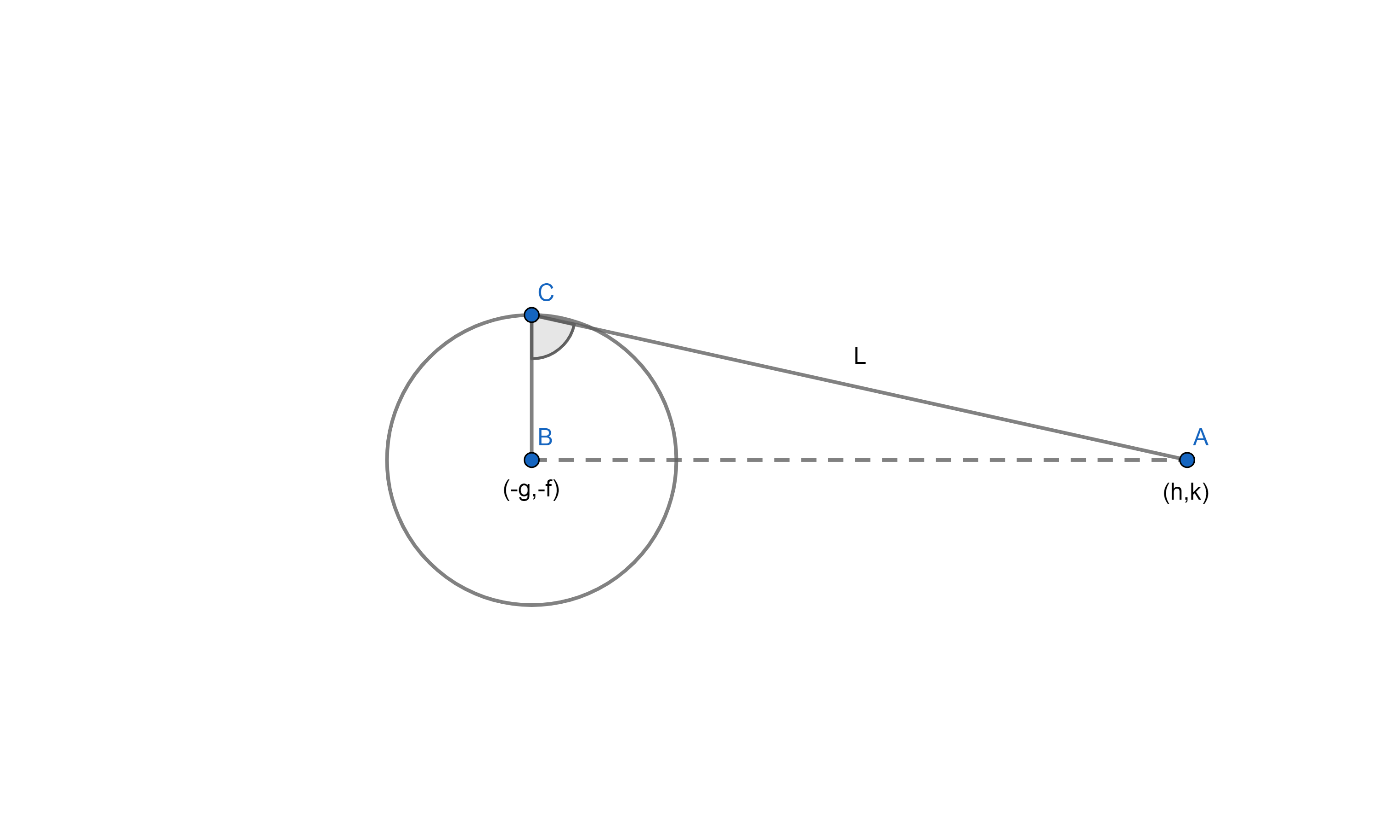
L= length of tangent $=\sqrt{A{{B}^{2}}-B{{C}^{2}}}$ (As ABC is a right angle triangle $AC\bot CB$ )
Hence, now coming to the question:
${{L}_{1}}=$ length of tangent from $\left( h,k \right)$ to first circle
$\begin{align}
& {{L}_{1}}=\sqrt{{{S}_{1}}}=\sqrt{{{h}^{2}}+{{k}^{2}}-16}.................\left( i \right) \\
& {{L}_{2}}=\sqrt{{{S}_{2}}}=\sqrt{{{h}^{2}}+{{k}^{2}}+2h+2k}.................\left( ii \right) \\
\end{align}$
As, it is given that length of tangent for the first circle is twice to the second circle i.e.,
${{L}_{1}}=2{{L}_{2}}$
\[\sqrt{{{h}^{2}}+{{k}^{2}}-16}=2\sqrt{{{h}^{2}}+{{k}^{2}}+2h+2k}\]
Squaring both sides
\[\begin{align}
& {{h}^{2}}+{{k}^{2}}-16=4\left( {{h}^{2}}+{{k}^{2}}+2h+2k \right) \\
& {{h}^{2}}+{{k}^{2}}-16=4{{h}^{2}}+4{{k}^{2}}+8h+8k \\
& 3{{h}^{2}}+3{{k}^{2}}+8h+8k+16=0 \\
\end{align}\]
Hence, Option C is the correct option.
Hence, we can get length of tangent as
$\begin{align}
& L=\sqrt{{{\left( h+g \right)}^{2}}+{{\left( k+f \right)}^{2}}-\left( {{g}^{2}}+{{f}^{2}}-C \right)} \\
& L=\sqrt{{{h}^{2}}+{{g}^{2}}+2hg+{{k}^{2}}+{{f}^{2}}+2kf-{{g}^{2}}-{{f}^{2}}+C} \\
& L=\sqrt{{{h}^{2}}+{{k}^{2}}+2gh+2kf+C} \\
\end{align}$
As we have equation;
$S={{x}^{2}}+{{y}^{2}}+2gx+2fy+C$
If we put $\left(h,k \right)$in place of $\left( x,y \right)$ we can get calculated ‘L’ by taking the root of $S\left( h,k \right)$.
Hence, Let ${{S}_{1}}={{h}^{2}}+{{k}^{2}}+2gh+2fk+C$
Then, $L=\sqrt{{{S}_{1}}}=\sqrt{{{h}^{2}}+{{k}^{2}}+2gh+2fk+C}$

Note: (i) If we do not use formula then we need to calculate length of tangent by using basic identities by which proof of length is done in solution.
(ii) One can make errors in the writing centre of the second circle. Sometimes, we take the centre $\left(g,f \right)\text{ or }\left( 2g,2f \right)$ from the standard equation of circle when we do very fast calculations.