Question

If the length of the parallel sides of a trapezium are $ 8cm $ , $ 9cm $ and the distance between the parallel sides is $ 6cm $ , then its area is
 $
  (a)\,51\,c{m^2} \\
  (b)\,68\,c{m^2} \\
  (c)\,34\,c{m^2} \\
  (d)\,72\,c{m^2} \\
  $

Answer 1

Hint: As, in a given problem we see that in trapezium both of its parallel sides as well as distance between them or we can say height of trapezium are given. Therefore, we can find the area of trapezium by using the standard formula of mensuration.
\[Area{\text{ }}of{\text{ }}trapezium{\text{ }} = \dfrac{1}{2} \cdot \left( {sum{\text{ of parallel side}}} \right) \times {\text{distance between them}}\]

Complete step-by-step answer:
Let ABCD is a trapezium in which AB and CD are parallel sides and AM is altitude from A on CD as shown in figure.

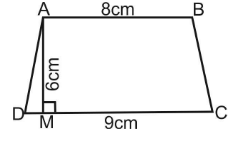
Therefore, we have
AB = $ 8cm $ , $ CD = 9cm $ and $ AM = 6cm $
We know that area of a trapezium when its parallel sides and distance between them are given can be calculated by using the standard area formula of mensuration. Which is as:
\[Area{\text{ }}of{\text{ }}trapezium{\text{ }} = \dfrac{1}{2} \cdot \left( {sum{\text{ of parallel side}}} \right) \times {\text{distance between them}}\]
Or we can write it as
Area of trapezium = $ \dfrac{1}{2}\left( {AB + CD} \right) \times AM $
Now, on substituting values in above formula. We have,
Area of trapezium = $ \dfrac{1}{2}\left( {8 + 9} \right) \times 6 $
 $ \Rightarrow Area\,\,of\,\,trapezium\,\, = \dfrac{1}{2}\left( {8 + 9} \right) \times 6 $
 $
   \Rightarrow Area\,\,of\,\,trapezium\,\, = \dfrac{1}{2} \times 17 \times 6 \\
   \Rightarrow Area\,\,of\,\,trapezium\,\, = 3 \times 17 \\
   \Rightarrow Area\,\,of\,\,trapezium\,\, = 51 \;
 $
Hence, from above we see that the area of trapezium of given dimension is $ 51\,c{m^2} $ .
Therefore, from the given four options. The correct option is option (a).
So, the correct answer is “Option A”.

Note: When in trapezium both of its parallel sides and distance between parallel sides or we can say altitude of trapezium are known, then we can find its area by dividing it into two triangles by joining either of its diagonal. And then finding the area of both triangles by formula $ \dfrac{1}{2} \times base \times altitude $ . Adding the area of two triangles gives an area of given trapezium.