Question

If the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement true or false? Why?

Answer 1

Hint: Start the solution by finding the angles subtended by the arcs at the centre of their respective circles using the property that the arc length is equal to $R\theta $ , where R is the radius of the circle and $\theta $ is the angle subtended by the arc at the centre. Then compare the results and reach the conclusion.

Complete step-by-step answer:
Let us start the solution by drawing the circles with radius r and radius 2r as given in the question for better visualisation.

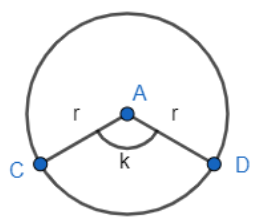
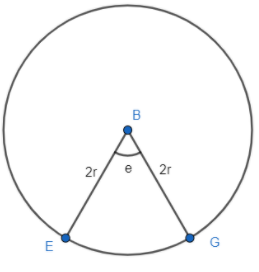
Now according to the question, let EG and CD be the arcs and k and e be the angles subtended by them at the centre of the respective circle.
Now we know that the length of the arc of a circle is given by is equal to $R\theta $ , where R is the radius of the circle and $\theta $ is the angle subtended by the arc at the centre.so, length of the arc CD and EG are:
$arc(CD)=rk$
$arc(EG)=2re$
Now as it is given in the question that arc length for both the circles are equal, we can say:
$arc(CD)=arc\left( EG \right)$
$\Rightarrow rk=2re$
$\Rightarrow k=2e$
So, it is clear that the angle subtended in the first circle is equal to double of the angle subtended by the equal arc in the second answer. So, the statement given in the question is true.

Note: Remember, the same relation is valid for the angle subtended at the circumference of the circle as well, because the angle subtended by an arc at the circumference of the circle are equal and half of the angle subtended at the centre. Also, make sure that you don’t give an answer without properly solving, because if you confuse angle subtended with the arc length, the answer would be different.