If the length of 3 sides of a Trapezium(other than base) are equal to 10cm, then find the area of the trapezium when it is maximum.
Answer
Verified583.5k+ views
Hint: Mark the 3 sides of 10cm. Now drop perpendiculars from the known parallel side to the unknown one. Now assume variable x to the extra part after perpendiculars. Now assume foot of perpendicular to P, Q. Thus apply formula for area of trapezium. Find its height by using Pythagoras theorem. Then you get area as a function of x. Now differentiate it to find the points of maximum by equating it to \[2\omega \]. By substituting back into area get the maximum area.
Complete step by step solution:
Given condition of trapezium in the question is written as:
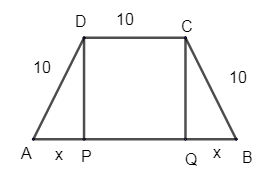
AD = DC = CB = 10
Draw perpendiculars DP & CQ on AB.
Let AP = x, by symmetry QB = x.
Let A be an area of trapezium. By formula we can say it as:
\[\Rightarrow A=\dfrac{1}{2}\times \] (sum of parallel sides) \[\times \] (height) – (1)
As triangle ADP is right angle by applying Pythagoras theorem we can write equation,
\[\Rightarrow A{{D}^{2}}=A{{P}^{2}}+D{{P}^{2}}\]
By substituting the value of sides into equation:
\[\Rightarrow {{10}^{2}}={{x}^{2}}+D{{P}^{2}}\]
By subtracting \[{{x}^{2}}\] on both sides we get it as:
\[\Rightarrow {{x}^{2}}+D{{P}^{2}}-{{x}^{2}}={{10}^{2}}-{{x}^{2}}\]
By cancelling common terms, we get it as follows here:
\[\Rightarrow D{{P}^{2}}={{10}^{2}}-{{x}^{2}}\]
By simplifying terms on right hand side, we get it as:
\[\Rightarrow D{{P}^{2}}=100-{{x}^{2}}\]
By applying square root on both sides, we get it as:
\[\Rightarrow \sqrt{D{{P}^{2}}}=\sqrt{100-{{x}^{2}}}\]
By simplifying the above equation of DP, we get it as:
\[\Rightarrow DP=\sqrt{100-{{x}^{2}}}\]
From diagram, we can see that DP = height, by this we get:
Height = \[\sqrt{100-{{x}^{2}}}\] - (2)
From the diagram we can see PQ = DC because of perpendiculars:
\[\Rightarrow \] PQ = DC = 10cm
By dividing AB by points P, Q points, we get it as:
\[\Rightarrow \] AB = AP + PQ + PB
By substituting the values of sides, we get it as:
\[\Rightarrow \] AB = x + 10 + x
By adding the term DC on both sides, we get it as:
\[\Rightarrow \] AB + DC = x + 10 + x + 10
By simplifying on right hand side, we get it as:
\[\Rightarrow \] AB + DC = 2 (x + 10)
By diagram we can say this is sum of parallel sides:
Sum of parallel sides = 2 (x + 10) – (3)
So, by this we found sum, height so we can find the area.
By substituting equation (2), (3) in equation (1), we get it as:
\[\Rightarrow A=\dfrac{1}{2}\times 2\left( x+10 \right)\times \sqrt{100-{{x}^{2}}}\]
By simplifying the terms, we can say the A to be:
\[\Rightarrow A=\left( x+10 \right)\times \sqrt{100-{{x}^{2}}}\] - (4)
We need to find the area of trapezium, at its maximum.
So, we need to maximize area, i.e. we need \[\dfrac{dA}{dx}=0\].
By differentiating on both sides with respect to x, we get:
\[\Rightarrow \dfrac{dA}{dx}=\dfrac{d}{dx}\left[ \left( x+10 \right)\sqrt{100-{{x}^{2}}} \right]\]
By basic knowledge of differentiation, u.v rule is said:
\[\Rightarrow d\left( u.v \right)=vdu+udv\]
By applying u.v rule here, we get the equation as:
\[\Rightarrow \dfrac{dA}{dx}=\sqrt{100-{{x}^{2}}}\dfrac{d}{dx}\left( x+10 \right)+\left( x+10 \right)\dfrac{d}{dx}\left( \sqrt{100-{{x}^{2}}} \right)\]
By basic knowledge of differentiation, we know that:
\[\Rightarrow \dfrac{d}{dx}\left( x \right)=1;\dfrac{d}{dx}\left( \sqrt{y} \right)=\dfrac{1}{2\sqrt{y}}\dfrac{dy}{dx}\]
By substituting these into the above equation, we get it as:
\[\Rightarrow \dfrac{dA}{dx}=\sqrt{100-{{x}^{2}}}.\left( 1 \right)+\left( x+10 \right)\dfrac{1}{2\sqrt{100-{{x}^{2}}}}.\dfrac{d}{dx}\left( 100-{{x}^{2}} \right)\]
By basic knowledge of differentiation, we know the formula:
\[\Rightarrow \dfrac{d}{dx}\left( k \right)=0\], k = constant, \[\dfrac{d}{dx}\left( -{{x}^{2}} \right)=-2x\].
By substituting these into above equation, we get it as:
\[\Rightarrow \dfrac{dA}{dx}=\sqrt{100-{{x}^{2}}}+\dfrac{\left( x+10 \right)}{2\sqrt{100-{{x}^{2}}}}\left( -2x \right)\]
By simplifying the second term, we get it as follows:
\[\Rightarrow \dfrac{dA}{dx}=\sqrt{100-{{x}^{2}}}-\dfrac{{{x}^{2}}+10x}{\sqrt{100-{{x}^{2}}}}\]
By taking least common multiple on left sides, we get it as:
\[\Rightarrow \dfrac{dA}{dx}=\dfrac{100-{{x}^{2}}-{{x}^{2}}-10x}{\sqrt{100-{{x}^{2}}}}\]
By substituting \[\dfrac{dA}{dx}=0\] and cross multiply we get it as:
\[\Rightarrow -2{{x}^{2}}-10x+100=0\]
By taking -2 as common, and writing 5x as 10x – 5x we get:
\[\Rightarrow {{x}^{2}}+10x-5x+50=0\]
Taking x common in first two terms and -5 common in next two terms we get:
\[\Rightarrow x\left( x+10 \right)-5\left( x+10 \right)=0\Rightarrow \left( x-5 \right)\left( x+10 \right)=0\]
By equation above, we can say the roots are given by:
x = 5 or x = 10 are the critical points. We have differentiation as:
\[\Rightarrow \dfrac{dA}{dx}=\dfrac{100-{{x}^{2}}-{{x}^{2}}-10x}{\sqrt{100-{{x}^{2}}}}\]
Now we need to differentiate again. By differentiating on both sides, we get:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{d\left( \dfrac{100-2{{x}^{2}}-10x}{\sqrt{100-{{x}^{2}}}} \right)}{dx}\]
Now by u, v rule, we can write it as:
\[\dfrac{d\left( \dfrac{u}{v} \right)}{dx}=\dfrac{vdu-udv}{{{v}^{2}}}\]
By substituting this equation, we get it in the form of:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{\sqrt{100-{{x}^{2}}}\left( d\left( -2{{x}^{2}}-10x+100 \right) \right)-\left( -2{{x}^{2}}-10x+100 \right)\left( d\left( \sqrt{100-{{x}^{2}}} \right) \right)}{100-{{x}^{2}}}\]
We know:
\[d\left( -2{{x}^{2}}-10x+100 \right)=-4x-10\]
\[d\left( \sqrt{100-{{x}^{2}}} \right)=\dfrac{-x}{\sqrt{100-{{x}^{2}}}}\]
By substituting this into above equation, we can write it as:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{\sqrt{100-{{x}^{2}}}\left( -4x-10 \right)-\left( -2{{x}^{2}}-10x+100 \right)\left( \dfrac{-x}{\sqrt{100-{{x}^{2}}}} \right)}{100-{{x}^{2}}}\]
By simplifying the above equation, we can write it as:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{\left( 100-{{x}^{2}} \right)\left( -4x-10 \right)-\left( -2{{x}^{2}}-10x+100 \right)\left( -x \right)}{\left( 100-{{x}^{2}} \right)\left( \sqrt{100-{{x}^{2}}} \right)}\]
By simplifying the numerator, we can write it as:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{\left( 4{{x}^{3}}-400x-1000+10{{x}^{2}} \right)-\left( 2{{x}^{3}}+10{{x}^{2}}-100x \right)}{\left( 100-{{x}^{2}} \right)\left( \sqrt{100-{{x}^{2}}} \right)}\]
By cancelling common terms we can write second differentiation as:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{2{{x}^{3}}-300x-1000}{\left( 100-{{x}^{2}} \right)\left( \sqrt{100-{{x}^{2}}} \right)}\]
If we substitute x = 5, we get it as:
\[\Rightarrow {{\left( \dfrac{{{d}^{2}}A}{d{{x}^{2}}} \right)}_{x=5}}=\dfrac{2{{\left( 5 \right)}^{3}}-300\left( 5 \right)-1000}{\left( 100-{{\left( 5 \right)}^{2}} \right)\left( \sqrt{100-{{\left( 5 \right)}^{2}}} \right)}\]
By simplifying above, we can say it as:
\[\Rightarrow {{\left( \dfrac{{{d}^{2}}A}{d{{x}^{2}}} \right)}_{x=5}}=\dfrac{-2250}{75\sqrt{75}}\]
Finally we can say value of it as:
\[\Rightarrow {{\left( \dfrac{{{d}^{2}}A}{d{{x}^{2}}} \right)}_{x=5}}=\dfrac{-30}{\sqrt{75}}\]
So, the second differentiation of A at x=5 is negative:
\[\Rightarrow {{\left( \dfrac{{{d}^{2}}A}{d{{x}^{2}}} \right)}_{x=5}}<0\Rightarrow \] x = 5 is maximum.
So, x = 5 is maximum. Substitute 5 in A, we get:
\[\Rightarrow A=\left( 5+10 \right)\sqrt{100-25}=15\sqrt{75}\]
By simplifying, we say it as: \[A=75\sqrt{3}\].
Therefore, the maximum area possible is \[75\sqrt{3}{{m}^{2}}\].
Note: The idea of dropping perpendiculars to divide A is because to maximize the area we need a variable whole AB can be assumed as variable. But then you want to get height in terms of assumed variables. So, this assumption we took here is the best one to solve it easily. After differentiating, find the critical parts carefully to get the correct result.
Complete step by step solution:
Given condition of trapezium in the question is written as:
AD = DC = CB = 10
Draw perpendiculars DP & CQ on AB.
Let AP = x, by symmetry QB = x.
Let A be an area of trapezium. By formula we can say it as:
\[\Rightarrow A=\dfrac{1}{2}\times \] (sum of parallel sides) \[\times \] (height) – (1)
As triangle ADP is right angle by applying Pythagoras theorem we can write equation,
\[\Rightarrow A{{D}^{2}}=A{{P}^{2}}+D{{P}^{2}}\]
By substituting the value of sides into equation:
\[\Rightarrow {{10}^{2}}={{x}^{2}}+D{{P}^{2}}\]
By subtracting \[{{x}^{2}}\] on both sides we get it as:
\[\Rightarrow {{x}^{2}}+D{{P}^{2}}-{{x}^{2}}={{10}^{2}}-{{x}^{2}}\]
By cancelling common terms, we get it as follows here:
\[\Rightarrow D{{P}^{2}}={{10}^{2}}-{{x}^{2}}\]
By simplifying terms on right hand side, we get it as:
\[\Rightarrow D{{P}^{2}}=100-{{x}^{2}}\]
By applying square root on both sides, we get it as:
\[\Rightarrow \sqrt{D{{P}^{2}}}=\sqrt{100-{{x}^{2}}}\]
By simplifying the above equation of DP, we get it as:
\[\Rightarrow DP=\sqrt{100-{{x}^{2}}}\]
From diagram, we can see that DP = height, by this we get:
Height = \[\sqrt{100-{{x}^{2}}}\] - (2)
From the diagram we can see PQ = DC because of perpendiculars:
\[\Rightarrow \] PQ = DC = 10cm
By dividing AB by points P, Q points, we get it as:
\[\Rightarrow \] AB = AP + PQ + PB
By substituting the values of sides, we get it as:
\[\Rightarrow \] AB = x + 10 + x
By adding the term DC on both sides, we get it as:
\[\Rightarrow \] AB + DC = x + 10 + x + 10
By simplifying on right hand side, we get it as:
\[\Rightarrow \] AB + DC = 2 (x + 10)
By diagram we can say this is sum of parallel sides:
Sum of parallel sides = 2 (x + 10) – (3)
So, by this we found sum, height so we can find the area.
By substituting equation (2), (3) in equation (1), we get it as:
\[\Rightarrow A=\dfrac{1}{2}\times 2\left( x+10 \right)\times \sqrt{100-{{x}^{2}}}\]
By simplifying the terms, we can say the A to be:
\[\Rightarrow A=\left( x+10 \right)\times \sqrt{100-{{x}^{2}}}\] - (4)
We need to find the area of trapezium, at its maximum.
So, we need to maximize area, i.e. we need \[\dfrac{dA}{dx}=0\].
By differentiating on both sides with respect to x, we get:
\[\Rightarrow \dfrac{dA}{dx}=\dfrac{d}{dx}\left[ \left( x+10 \right)\sqrt{100-{{x}^{2}}} \right]\]
By basic knowledge of differentiation, u.v rule is said:
\[\Rightarrow d\left( u.v \right)=vdu+udv\]
By applying u.v rule here, we get the equation as:
\[\Rightarrow \dfrac{dA}{dx}=\sqrt{100-{{x}^{2}}}\dfrac{d}{dx}\left( x+10 \right)+\left( x+10 \right)\dfrac{d}{dx}\left( \sqrt{100-{{x}^{2}}} \right)\]
By basic knowledge of differentiation, we know that:
\[\Rightarrow \dfrac{d}{dx}\left( x \right)=1;\dfrac{d}{dx}\left( \sqrt{y} \right)=\dfrac{1}{2\sqrt{y}}\dfrac{dy}{dx}\]
By substituting these into the above equation, we get it as:
\[\Rightarrow \dfrac{dA}{dx}=\sqrt{100-{{x}^{2}}}.\left( 1 \right)+\left( x+10 \right)\dfrac{1}{2\sqrt{100-{{x}^{2}}}}.\dfrac{d}{dx}\left( 100-{{x}^{2}} \right)\]
By basic knowledge of differentiation, we know the formula:
\[\Rightarrow \dfrac{d}{dx}\left( k \right)=0\], k = constant, \[\dfrac{d}{dx}\left( -{{x}^{2}} \right)=-2x\].
By substituting these into above equation, we get it as:
\[\Rightarrow \dfrac{dA}{dx}=\sqrt{100-{{x}^{2}}}+\dfrac{\left( x+10 \right)}{2\sqrt{100-{{x}^{2}}}}\left( -2x \right)\]
By simplifying the second term, we get it as follows:
\[\Rightarrow \dfrac{dA}{dx}=\sqrt{100-{{x}^{2}}}-\dfrac{{{x}^{2}}+10x}{\sqrt{100-{{x}^{2}}}}\]
By taking least common multiple on left sides, we get it as:
\[\Rightarrow \dfrac{dA}{dx}=\dfrac{100-{{x}^{2}}-{{x}^{2}}-10x}{\sqrt{100-{{x}^{2}}}}\]
By substituting \[\dfrac{dA}{dx}=0\] and cross multiply we get it as:
\[\Rightarrow -2{{x}^{2}}-10x+100=0\]
By taking -2 as common, and writing 5x as 10x – 5x we get:
\[\Rightarrow {{x}^{2}}+10x-5x+50=0\]
Taking x common in first two terms and -5 common in next two terms we get:
\[\Rightarrow x\left( x+10 \right)-5\left( x+10 \right)=0\Rightarrow \left( x-5 \right)\left( x+10 \right)=0\]
By equation above, we can say the roots are given by:
x = 5 or x = 10 are the critical points. We have differentiation as:
\[\Rightarrow \dfrac{dA}{dx}=\dfrac{100-{{x}^{2}}-{{x}^{2}}-10x}{\sqrt{100-{{x}^{2}}}}\]
Now we need to differentiate again. By differentiating on both sides, we get:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{d\left( \dfrac{100-2{{x}^{2}}-10x}{\sqrt{100-{{x}^{2}}}} \right)}{dx}\]
Now by u, v rule, we can write it as:
\[\dfrac{d\left( \dfrac{u}{v} \right)}{dx}=\dfrac{vdu-udv}{{{v}^{2}}}\]
By substituting this equation, we get it in the form of:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{\sqrt{100-{{x}^{2}}}\left( d\left( -2{{x}^{2}}-10x+100 \right) \right)-\left( -2{{x}^{2}}-10x+100 \right)\left( d\left( \sqrt{100-{{x}^{2}}} \right) \right)}{100-{{x}^{2}}}\]
We know:
\[d\left( -2{{x}^{2}}-10x+100 \right)=-4x-10\]
\[d\left( \sqrt{100-{{x}^{2}}} \right)=\dfrac{-x}{\sqrt{100-{{x}^{2}}}}\]
By substituting this into above equation, we can write it as:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{\sqrt{100-{{x}^{2}}}\left( -4x-10 \right)-\left( -2{{x}^{2}}-10x+100 \right)\left( \dfrac{-x}{\sqrt{100-{{x}^{2}}}} \right)}{100-{{x}^{2}}}\]
By simplifying the above equation, we can write it as:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{\left( 100-{{x}^{2}} \right)\left( -4x-10 \right)-\left( -2{{x}^{2}}-10x+100 \right)\left( -x \right)}{\left( 100-{{x}^{2}} \right)\left( \sqrt{100-{{x}^{2}}} \right)}\]
By simplifying the numerator, we can write it as:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{\left( 4{{x}^{3}}-400x-1000+10{{x}^{2}} \right)-\left( 2{{x}^{3}}+10{{x}^{2}}-100x \right)}{\left( 100-{{x}^{2}} \right)\left( \sqrt{100-{{x}^{2}}} \right)}\]
By cancelling common terms we can write second differentiation as:
\[\Rightarrow \dfrac{{{d}^{2}}A}{d{{x}^{2}}}=\dfrac{2{{x}^{3}}-300x-1000}{\left( 100-{{x}^{2}} \right)\left( \sqrt{100-{{x}^{2}}} \right)}\]
If we substitute x = 5, we get it as:
\[\Rightarrow {{\left( \dfrac{{{d}^{2}}A}{d{{x}^{2}}} \right)}_{x=5}}=\dfrac{2{{\left( 5 \right)}^{3}}-300\left( 5 \right)-1000}{\left( 100-{{\left( 5 \right)}^{2}} \right)\left( \sqrt{100-{{\left( 5 \right)}^{2}}} \right)}\]
By simplifying above, we can say it as:
\[\Rightarrow {{\left( \dfrac{{{d}^{2}}A}{d{{x}^{2}}} \right)}_{x=5}}=\dfrac{-2250}{75\sqrt{75}}\]
Finally we can say value of it as:
\[\Rightarrow {{\left( \dfrac{{{d}^{2}}A}{d{{x}^{2}}} \right)}_{x=5}}=\dfrac{-30}{\sqrt{75}}\]
So, the second differentiation of A at x=5 is negative:
\[\Rightarrow {{\left( \dfrac{{{d}^{2}}A}{d{{x}^{2}}} \right)}_{x=5}}<0\Rightarrow \] x = 5 is maximum.
So, x = 5 is maximum. Substitute 5 in A, we get:
\[\Rightarrow A=\left( 5+10 \right)\sqrt{100-25}=15\sqrt{75}\]
By simplifying, we say it as: \[A=75\sqrt{3}\].
Therefore, the maximum area possible is \[75\sqrt{3}{{m}^{2}}\].
Note: The idea of dropping perpendiculars to divide A is because to maximize the area we need a variable whole AB can be assumed as variable. But then you want to get height in terms of assumed variables. So, this assumption we took here is the best one to solve it easily. After differentiating, find the critical parts carefully to get the correct result.
Recently Updated Pages
Two men on either side of the cliff 90m height observe class 10 maths CBSE
What happens to glucose which enters nephron along class 10 biology CBSE
Cutting of the Chinese melon means A The business and class 10 social science CBSE
Write a dialogue with at least ten utterances between class 10 english CBSE
Show an aquatic food chain using the following organisms class 10 biology CBSE
A circle is inscribed in an equilateral triangle and class 10 maths CBSE
Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE
Write a letter to the principal requesting him to grant class 10 english CBSE
What is the median of the first 10 natural numbers class 10 maths CBSE
The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths
Which of the following does not have a fundamental class 10 physics CBSE
State and prove converse of BPT Basic Proportionality class 10 maths CBSE