Question

If the incircle of $\Delta ABC$ touches its sides, respectively at $L,M$ and $N$ . If $x,y,z$ are the circumradius of the triangles $MIN,NIL$ and $LIM$ , where $I$ is the incentre, then find $xyz=$ .
(a) $\dfrac{{{r}^{2}}R}{4}$
(b) $\dfrac{1}{2}R{{r}^{2}}$
(c) $R{{r}^{2}}$
(d) $\dfrac{1}{2}R{{r}^{3}}$

Answer 1

Hint: For solving this question we will use the formula of the Sine Rule $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$ . After that, we will try to find the value of $x,y,z$ separately in terms of $r,\sin \dfrac{A}{2},\sin \dfrac{B}{2}$ and $\sin \dfrac{C}{2}$ . And in the end, we will use the formula $\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}=\dfrac{r}{4R}$ to find the value of $xyz$ in terms of its incircle radius $\left( r \right)$ and circumcircle radius $\left( R \right)$ .

Complete step-by-step answer:
Given:
It is given that there is a $\Delta ABC$ and its incircle touches its sides, respectively at $L,M$ and $N$ . If $x,y,z$ are the circumradius of the triangles $MIN,NIL$ and $LIM$ , where $I$ is the incentre, and we have to find the value of $xyz$ in terms of its incircle radius $\left( r \right)$ and circumcircle radius $\left( R \right)$ . For more clarity look at the figure given below:

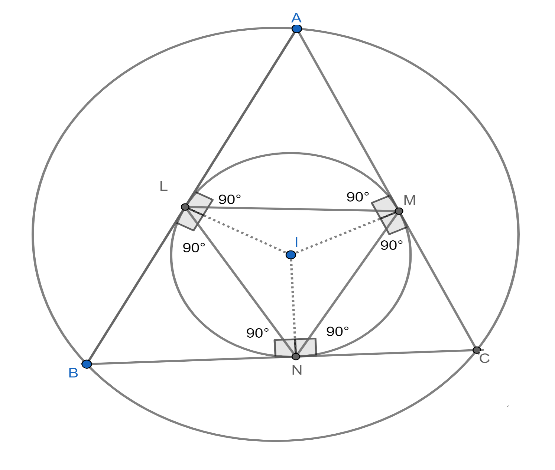
In the above figure, $R$ is the radius of the circumcircle and $r$ is the radius of the incircle of the $\Delta ABC$ , where $BC=a$ , $AC=b$ , $AB=c$ , $\angle ABC=\angle B$ , $\angle BAC=\angle A$ and $\angle ACB=\angle C$ . Then,

$MI=NI=LI=r..............\left( 1 \right)$

Now, before we proceed we should know the following formulas:

$\begin{align}

  & \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\text{ }\left( \text{Sine Rule} \right) \\

 & \sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}=\dfrac{r}{4R}.................\left( 2 \right) \\

\end{align}$

Now, we will find the value of $x,y,z$ separately and then, we will find the value of $xyz$ in terms of its incircle radius $\left( r \right)$ and circumcircle radius $\left( R \right)$ .

Calculation of $x$ :

Look at the figure given below:

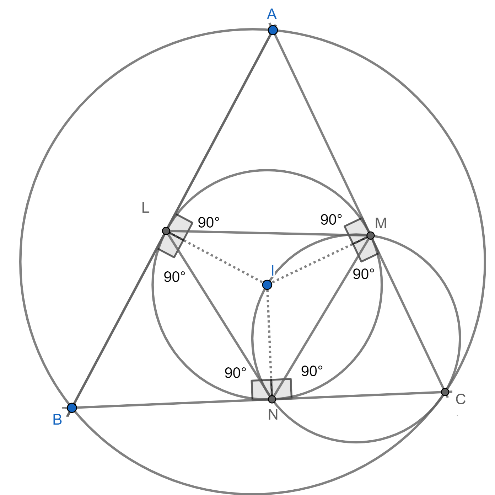
Now, in the quadrilateral MINC, we know that $\angle INC=\angle IMC={{90}^{0}}$ . And as we know that, the sum of internal angles of the quadrilateral is ${{360}^{0}}$ . Then,

$\begin{align}

  & \angle INC+\angle IMC+\angle MIN+\angle MCN={{360}^{0}} \\

 & \Rightarrow {{90}^{0}}+{{90}^{0}}+\angle MIN+\angle MCN={{360}^{0}} \\

 & \Rightarrow \angle MIN+\angle MCN={{180}^{0}} \\

\end{align}$

Now, from the above figure, we can write $\angle MCN=\angle ACB=\angle C$ in the above equation. Then,

$\begin{align}

  & \angle MIN+\angle MCN={{180}^{0}} \\

 & \Rightarrow \angle MIN+\angle C={{180}^{0}} \\

 & \Rightarrow \angle MIN={{180}^{0}}-\angle C.............\left( 3 \right) \\

\end{align}$

Now, in $\Delta MIN$ from equation (1), we can write that $MI=NI=r$ which means it is an isosceles triangle and as we know that, angles opposite to equal sides of an isosceles triangle are equal. Then,

$\angle INM=\angle IMN.............\left( 4 \right)$

Now, we know that for any triangle sum of its internal angles is ${{180}^{0}}$ . Then,
$\angle MIN+\angle INM+\angle IMN={{180}^{0}}$

Now, put $\angle MIN={{180}^{0}}-\angle C$ from equation (3) and $\angle INM=\angle IMN$ from equation (4) in the above equation. Then,

$\begin{align}

  & \angle MIN+\angle INM+\angle IMN={{180}^{0}} \\

 & \Rightarrow {{180}^{0}}-\angle C+\angle IMN+\angle IMN={{180}^{0}} \\

 & \Rightarrow 2\angle IMN=\angle C \\

 & \Rightarrow \angle IMN=\dfrac{\angle C}{2}......................\left( 5 \right) \\

\end{align}$

Now, as it is given that $x$ is the radius of the circumcircle of $\Delta MIN$ so, we can use Sine Rule. Then,

$\dfrac{NI}{\sin \left( \angle IMN \right)}=2x$

Now, put $NI=r$ from equation (1) and $\angle IMN=\dfrac{\angle C}{2}$ from equation (5) in the above equation. Then,

$\begin{align}

  & \dfrac{NI}{\sin \left( \angle IMN \right)}=2x \\

 & \Rightarrow \dfrac{r}{\sin \dfrac{C}{2}}=2x \\

 & \Rightarrow x=\dfrac{r}{2\sin \dfrac{C}{2}}..............................\left( 6 \right) \\
\end{align}$

Calculation of $y$ :

Look at the figure given below:

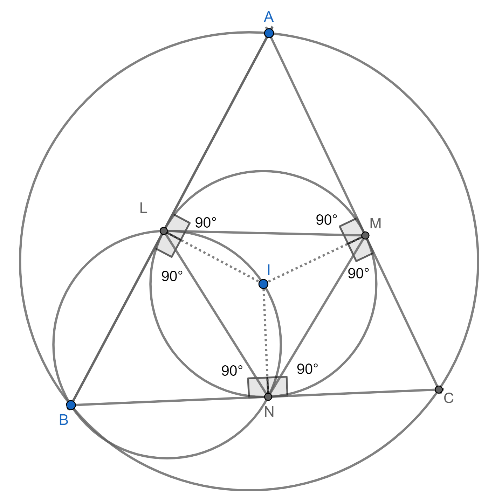
Now, in the quadrilateral LINB, we know that $\angle INB=\angle ILB={{90}^{0}}$ . And as we know that the sum of internal angles of the quadrilateral is ${{360}^{0}}$ . Then,

$\begin{align}

  & \angle INB+\angle ILB+\angle LIN+\angle LBN={{360}^{0}} \\

 & \Rightarrow {{90}^{0}}+{{90}^{0}}+\angle LIN+\angle LBN={{360}^{0}} \\

 & \Rightarrow \angle LIN+\angle LBN={{180}^{0}} \\

\end{align}$

Now, from the above figure, we can write $\angle LBN=\angle ABC=\angle B$ in the above equation. Then,

$\begin{align}

  & \angle LIN+\angle LBN={{180}^{0}} \\

 & \Rightarrow \angle LIN+\angle B={{180}^{0}} \\

 & \Rightarrow \angle LIN={{180}^{0}}-\angle B.............\left( 7 \right) \\

\end{align}$

Now, in $\Delta LIN$ from equation (1), we can write that $LI=NI=r$ which means it is an isosceles triangle and as we know that, angles opposite to equal sides of an isosceles triangle are equal. Then,

$\angle INL=\angle ILN.............\left( 8 \right)$

Now, we know that for any triangle sum of its internal angles is ${{180}^{0}}$ . Then,

$\angle LIN+\angle INL+\angle ILN={{180}^{0}}$

Now, put $\angle LIN={{180}^{0}}-\angle B$ from equation (7) and $\angle INL=\angle ILN$ from equation (8) in the above equation. Then,

$\begin{align}

  & \angle LIN+\angle INL+\angle ILN={{180}^{0}} \\

 & \Rightarrow {{180}^{0}}-\angle B+\angle ILN+\angle ILN={{180}^{0}} \\

 & \Rightarrow 2\angle ILN=\angle B \\

 & \Rightarrow \angle ILN=\dfrac{\angle B}{2}......................\left( 9 \right) \\

\end{align}$

Now, as it is given that $y$ is the radius of the circumcircle of $\Delta LIN$ so, we can use Sine Rule. Then,

$\dfrac{NI}{\sin \left( \angle ILN \right)}=2y$

Now, put $NI=r$ from equation (1) and $\angle ILN=\dfrac{\angle B}{2}$ from equation (9) in the above equation. Then,

$\begin{align}

  & \dfrac{NI}{\sin \left( \angle ILN \right)}=2y \\

 & \Rightarrow \dfrac{r}{\sin \dfrac{B}{2}}=2y \\

 & \Rightarrow y=\dfrac{r}{2\sin \dfrac{B}{2}}..............................\left( 10 \right) \\
\end{align}$

Calculation of $z$ :

Look at the figure given below:

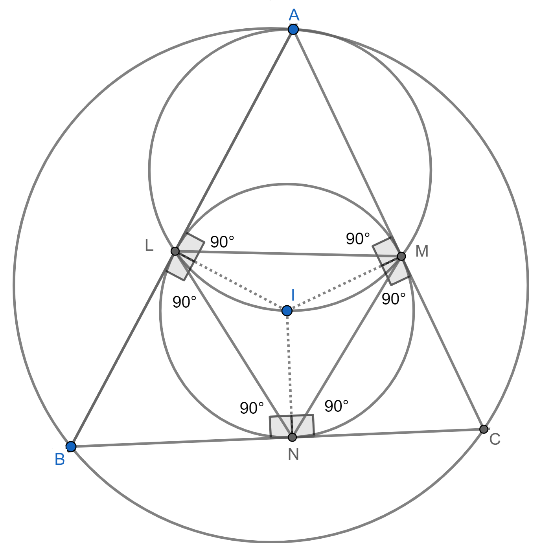
Now, in the quadrilateral LIMA, we know that $\angle IMA=\angle ILA={{90}^{0}}$ . And as we know that the sum of internal angles of the quadrilateral is ${{360}^{0}}$ . Then,

$\begin{align}

  & \angle IMA+\angle ILA+\angle LIM+\angle LAN={{360}^{0}} \\

 & \Rightarrow {{90}^{0}}+{{90}^{0}}+\angle LIM+\angle LAN={{360}^{0}} \\

 & \Rightarrow \angle LIM+\angle LAN={{180}^{0}} \\

\end{align}$

Now, from the above figure, we can write $\angle LAN=\angle BAC=\angle A$ in the above equation. Then,

$\begin{align}

  & \angle LIM+\angle LAN={{180}^{0}} \\

 & \Rightarrow \angle LIM+\angle A={{180}^{0}} \\

 & \Rightarrow \angle LIM={{180}^{0}}-\angle A.............\left( 11 \right) \\

\end{align}$

Now, in $\Delta LIM$ from equation (1), we can write that $LI=MI=r$ which means it is an isosceles triangle and as we know that, angles opposite to equal sides of an isosceles triangle are equal. Then,

$\angle IML=\angle ILM.............\left( 12 \right)$

Now, we know that for any triangle sum of its internal angles is ${{180}^{0}}$ . Then,

$\angle LIM+\angle IML+\angle ILM={{180}^{0}}$

Now, put $\angle LIM={{180}^{0}}-\angle A$ from equation (11) and $\angle IML=\angle ILM$ from equation (12) in the above equation. Then,

$\begin{align}

  & \angle LIM+\angle IML+\angle ILM={{180}^{0}} \\

 & \Rightarrow {{180}^{0}}-\angle A+\angle ILM+\angle ILM={{180}^{0}} \\

 & \Rightarrow 2\angle ILM=\angle A \\

 & \Rightarrow \angle ILM=\dfrac{\angle A}{2}......................\left( 13 \right) \\

\end{align}$

Now, as it is given that $z$ is the radius of the circumcircle of $\Delta LIM$ so, we can use Sine Rule. Then,

$\dfrac{MI}{\sin \left( \angle ILM \right)}=2z$

Now, put $NI=r$ from equation (1) and $\angle ILM=\dfrac{\angle A}{2}$ from equation (13) in the above equation. Then,

$\begin{align}

  & \dfrac{MI}{\sin \left( \angle ILM \right)}=2z \\

 & \Rightarrow \dfrac{r}{\sin \dfrac{A}{2}}=2z \\

 & \Rightarrow z=\dfrac{r}{2\sin \dfrac{A}{2}}..............................\left( 14 \right) \\

\end{align}$

Now, from the equation (6), (10) and (14), we will find the value of $xyz$ . Then,

$\begin{align}

  & xyz=\dfrac{r}{2\sin \dfrac{C}{2}}\times \dfrac{r}{2\sin \dfrac{B}{2}}\times \dfrac{r}{2\sin \dfrac{A}{2}} \\

 & \Rightarrow xyz=\dfrac{{{r}^{3}}}{8\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}} \\

\end{align}$

Now, put $\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}=\dfrac{r}{4R}$ from equation (2) in the above equation. Then,

$\begin{align}

  & xyz=\dfrac{{{r}^{3}}}{8\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}} \\

 & \Rightarrow xyz=\dfrac{{{r}^{3}}}{8\times \dfrac{r}{4R}} \\

 & \Rightarrow xyz=\dfrac{{{r}^{2}}R}{2} \\

\end{align}$

Now, from the above result, we conclude that the value of $xyz=\dfrac{1}{2}R{{r}^{2}}$ .
Hence, (b) will be the correct option.


Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer. After that, we should proceed in a stepwise manner for smooth calculation and apply each formula accurately without any error. Moreover, in the problem of the solution of triangles, we should always draw the figure as per the data given in the question for better understanding and solve without any error.