Question

If the function $f\left( x \right)=\sin \left( \log x \right)-\cos \left( \log x \right)$ strictly increase in the interval $\left( {{e}^{\lambda }},{{e}^{\mu }} \right)$ then the value of $-500\cos \left( \mu -\lambda \right)$.

Answer 1

Hint: We will first find the differentiation of the given function as we have given that the function strictly increases in the interval. Form that condition we will find the range of $x$ and we equate the result range with the given range to find the values of $\lambda ,\mu $ from that values we can find the required value of $-500\cos \left( \mu -\lambda \right)$

Complete step by step answer:
Given that, $f\left( x \right)=\sin \left( \log x \right)-\cos \left( \log x \right)$ strictly increase in the interval $\left( {{e}^{\lambda }},{{e}^{\mu }} \right)$, then
${{f}^{'}}\left( x \right)\text{ }>\text{ }0$
The value of ${{f}^{'}}\left( x \right)$ is
$\begin{align}
  & {{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left[ \sin \left( \log x \right)-\cos \left( \log x \right) \right] \\
 & =\dfrac{d}{dx}\left[ \sin \left( \log x \right) \right]-\dfrac{d}{dx}\left[ \cos \left( \log x \right) \right]
\end{align}$
Use the formulas $\dfrac{d}{dx}\left( \sin x \right)=\cos x$, $\dfrac{d}{dx}\left( \cos x \right)=-\sin x$ in the above equation, then
${{f}^{'}}\left( x \right)=\cos \left( \log x \right).\dfrac{d}{dx}\left( \log x \right)+\sin \left( \log x \right)\dfrac{d}{dx}\left( \log x \right)$
Use the formula $\dfrac{d}{dx}\left( \log x \right)=\dfrac{1}{x}$, then
$\begin{align}
  & {{f}^{'}}\left( x \right)=\cos \left( \log x \right).\dfrac{1}{x}+\sin \left( \log x \right).\dfrac{1}{x} \\
 & =\dfrac{1}{x}\left[ \cos \left( \log x \right)+\sin \left( \log x \right) \right]
\end{align}$
if the function $f\left( x \right)$ strictly increase in the interval $\left( {{e}^{\lambda }},{{e}^{\mu }} \right)$, then
$\begin{align}
  & {{f}^{'}}\left( x \right)\text{ }>\text{ }0 \\
 & \dfrac{1}{x}\left[ \sin \left( \log x \right)+\cos \left( \log x \right) \right]\text{ }>\text{ }0 \\
 & \sin \left( \log x \right)+\cos \left( \log x \right)\text{ }>\text{ }0
\end{align}$
Multiply and divide by $\sqrt{2}$ in the above expression, then we have
$\sqrt{2}\left( \dfrac{1}{\sqrt{2}}\sin \left( \log x \right)+\dfrac{1}{\sqrt{2}}\cos \left( \log x \right) \right)\text{ }>\text{ }0$
Substituting $\sin \dfrac{\pi }{4}=\cos \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}$in the above expression, then
$\cos \dfrac{\pi }{4}.\sin \left( \log x \right)+\sin \dfrac{\pi }{4}\cos \left( \log x \right)\text{ }>\text{ }0$
Using the formula $\sin x.\cos y+\cos x.\sin y=\sin \left( x+y \right)$ in the above expression, then we have
$\sin \left( \dfrac{\pi }{4}+\log x \right)\text{ }>\text{ }0$
The graph of $y=\sin x$ is given below

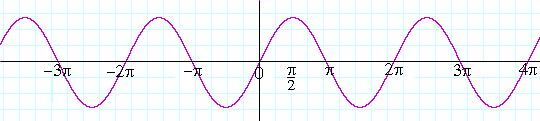
Form the above equation we have value of $\sin x\text{ }>\text{ }0$ for $0\text{ }<\text{ }x\text{ }<\text{ }\pi $, so the value of $\sin \left( \dfrac{\pi }{4}+\log x \right)\text{ }>\text{ }0$
For
$\begin{align}
  & 0\text{ }<\text{ }\dfrac{\pi }{4}+\log x\text{ }<\text{ }\pi \\
 & -\dfrac{\pi }{4}\text{ }<\text{ }\log x\text{ }<\text{ }\pi -\dfrac{\pi }{4} \\
 & -\dfrac{\pi }{4}\text{ }<\text{ }\log x\text{ }<\text{ }\dfrac{3\pi }{4} \\
 & {{e}^{-\dfrac{\pi }{4}}}\text{ }<\text{ }x\text{ }<\text{ }{{e}^{\dfrac{3\pi }{4}}}
\end{align}$
$\therefore $$x\in \left( {{e}^{-\dfrac{\pi }{4}}},{{e}^{\dfrac{3\pi }{4}}} \right)$
But given that $x\in \left( {{e}^{\lambda }},{{e}^{\mu }} \right)$ hence the values of $\lambda ,\mu $ are
$\lambda =-\dfrac{\pi }{4}$ and $\mu =\dfrac{3\pi }{4}$
Now the value of $-500\cos \left( \mu -\lambda \right)$ is
$\begin{align}
  & -500\cos \left( \mu -\lambda \right)=-500\cos \left( \dfrac{3\pi }{4}-\left( -\dfrac{\pi }{4} \right) \right) \\
 & =-500\cos \left( \dfrac{3\pi }{4}+\dfrac{\pi }{4} \right) \\
 & =-500\cos \pi \\
 & =-500\left( -1 \right) \\
 & =500
\end{align}$

Note: Please take the limits of $x$ for $\sin x\text{ }>\text{ }0$ as $0\text{ }<\text{ }x\text{ }<\text{ }\pi $. We have other ranges also for $x$ but it is the basic to consider the range from $0\text{ }<\text{ }x\text{ }<\text{ }\pi $. Be aware of the operations that we follow to simplify the range. The derivative of $\log x$ is $\dfrac{1}{x}$, mathematically $\dfrac{d}{dx}\left( \log x \right)=\dfrac{1}{x}$ and the differentiation of the functions like $f\left( g\left( x \right) \right)$ is given by $\dfrac{d}{dx}\left( f\left( g\left( x \right) \right) \right)={{f}^{'}}\left( g\left( x \right) \right).{{g}^{'}}\left( x \right)$