
If the following matrix follows a certain rule row wise or column-wise , find the missing number. \[\]
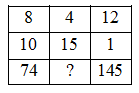
A.112\[\]
B.82\[\]
C.14\[\]
D.31\[\]

Answer
584.1k+ views
Hint: We try to guess the relationship with arithmetic operations in the row-wise first and observe that we cannot find a consistent relationship. We guess the rule column-wise and see that the numbers in the third row are large numbers compared to the first and second row. We guess a rule with addition, multiplication, and square to get the missing number.\[\]
Complete step by step answer:
We have the given matrix in the question .\[\]
We see that there are three numbers in the first row 8,4,12 as well as in second row 10,15,1. The third row has 74 in the first column and 145 in third column and in second column is the missing number which we are asked to find. \[\]
We know from the question that there is a relationship between row-wise or column-wise. We also know that in problems of this type we have to use arithmetic operations among the numbers in the row or the column to guess that relationship. We use addition, multiplication, square to reach a larger number than the operands and subtraction,division, square root to reach a smaller number than the operands. \[\]
Let us check if it is any relationship row-wise. We have the numbers 8,4,12 in the first row and 10,15,1 in the second row. We see that the number 4 is smaller than 8 and 12 in first row while the number 15 is larger than 10 and 1. So the same operations and hence rule cannot be used in both rows. We guess that we cannot find the same rule for every row. \[\]
Let us check if there is any relationship column-wise. We have the numbers 8,10,74 in the first column and 12, 1, 145 in the second column. We see that 74 as well 145 are greater numbers then the pair of numbers right above. We can reach a larger number by addition, multiplication, and square. We use the rule ${{8}^{2}}+10=74$ in first column and check the third column with the same rule and have ${{12}^{2}}+1=145$. So the rule satisfies. We use the rule in the second column ad get ${{4}^{2}}+15=31$ and 31 is in option D. So the missing number is 31. \[\]
Note:
If the numbers in the third row would have been very large we would have tried to guess a relationship with cubes of the entries and they would have been very small we would have used cube root.
Complete step by step answer:
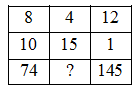
We have the given matrix in the question .\[\]

We see that there are three numbers in the first row 8,4,12 as well as in second row 10,15,1. The third row has 74 in the first column and 145 in third column and in second column is the missing number which we are asked to find. \[\]
We know from the question that there is a relationship between row-wise or column-wise. We also know that in problems of this type we have to use arithmetic operations among the numbers in the row or the column to guess that relationship. We use addition, multiplication, square to reach a larger number than the operands and subtraction,division, square root to reach a smaller number than the operands. \[\]
Let us check if it is any relationship row-wise. We have the numbers 8,4,12 in the first row and 10,15,1 in the second row. We see that the number 4 is smaller than 8 and 12 in first row while the number 15 is larger than 10 and 1. So the same operations and hence rule cannot be used in both rows. We guess that we cannot find the same rule for every row. \[\]
Let us check if there is any relationship column-wise. We have the numbers 8,10,74 in the first column and 12, 1, 145 in the second column. We see that 74 as well 145 are greater numbers then the pair of numbers right above. We can reach a larger number by addition, multiplication, and square. We use the rule ${{8}^{2}}+10=74$ in first column and check the third column with the same rule and have ${{12}^{2}}+1=145$. So the rule satisfies. We use the rule in the second column ad get ${{4}^{2}}+15=31$ and 31 is in option D. So the missing number is 31. \[\]
Note:
If the numbers in the third row would have been very large we would have tried to guess a relationship with cubes of the entries and they would have been very small we would have used cube root.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




