Question

If the first minima in Young’s double-slit experiment occur directly in front of the slits (distance between slit and screen \[D = 12cm\] and distance between slits \[d = 5cm\], then the wavelength of the radiation used can be
A. \[2cm\]
B. \[4cm\]
C. \[\dfrac{2}{3}cm\]
D. \[\dfrac{4}{3}cm\]

Answer 1

Hint: Superposition principle says when two or more waves overlap in space, the resultant disturbance is the sum of the individual disturbances.
In this question, it is given that a first minimum obtained on the screen is directly in front of the slits; hence we have to find the wavelength of the radiation given as \[\vartriangle x = \left( {2n - 1} \right)\dfrac{\lambda }{2}\]. First we need to evaluate the distance travelled by the radiated light in between the two slits one by one and then, equating their difference with the formula \[\vartriangle x = \left( {2n - 1} \right)\dfrac{\lambda }{2}\] to get the result.

Complete step by step solution:
Distance between screen and slit \[D = 12cm\]
Distance between slits \[d = 5cm\]
First minima fall directly in front of the slit \[{S_1}\] at point P

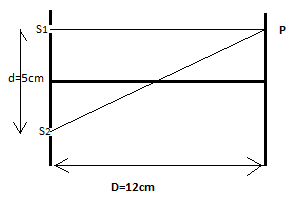
Distance travelled by wave from \[{S_1}\]to \[{S_1}P\]\[ = 12cm\]
The path travelled by light from slit \[{S_2}\]to \[{S_2}P\]\[ = \sqrt {{D^2} + {d^2}} = \sqrt {{{12}^2} + {5^2}} = \sqrt {144 + 25} = \sqrt {169} = 13cm\]
So the path difference between two minima \[\vartriangle x = {S_2}P - {S_1}P = 13 - 12 = 1cm\]
Given the point for first minima\[\left( {n = 1} \right)\], \[\vartriangle x = \left( {2n - 1} \right)\dfrac{\lambda }{2} = \left( {2 \times x - 1} \right)\dfrac{\lambda }{2} = \dfrac{\lambda }{2}\]
Hence we can write:
 \[
  \vartriangle x = \dfrac{\lambda }{2} \\
  \dfrac{\lambda }{2} = 1 \\
  \lambda = 2cm \\
 \]

Hence the wavelength of the radiation is 2cm Option A.

Note: A point on the screen where the wave crest of one wave falls on the wave crest of other, the resultant amplitude is maxima. A point on the screen where the wave crest of one falls on the wave trough of another, the resulting amplitude is minima.