
If the family of lines $x\left( a+2b \right)+y\left( 3a+b \right)=a+b$ passes through the point for all values of $a$ and $b$, then the coordinates of the points is:\[\]
A.$\left( 2,1 \right)$\[\]
B.$\left( 2,-1 \right)$\[\]
C.$\left( -2,1 \right)$\[\]
D. None of these \[\]
Answer
570.6k+ views
Hint: We treat $a$ and $b$ as variables and open the brackets in the left hand side of the given equation of line and take $a$ and $b$ common. We equate the coefficients of $a$ and $b$ from both sides of the equation to get two linear equations in $x$ and $y$ which we solve to get the coordinate of the required point. \[\]
Complete step-by-step answer:
We are given the question that the family of lines $x\left( a+2b \right)+y\left( 3a+b \right)=a+b$ passes through the a fixed point for all values of $a$ and $b$. Let us open the brackets in the left hand side and simplify to
\[\begin{align}
& x\left( a+2b \right)+y\left( 3a+b \right)=a+b \\
& \Rightarrow xa+2bx+3ay+by=a+b \\
\end{align}\]
We take $a$ and $b$ common in the left hand side of the equation in the above step in the above step to have;
\[\Rightarrow a\left( x+y \right)+b\left( 2x+3y \right)=a\cdot 1+b\cdot 1\]
We compare the coefficients of $a,b$ from both side of the question in the above step to have;
\[\begin{align}
& x+y=1.....\left( 1 \right) \\
& 2x+3y=1.....\left( 2 \right) \\
\end{align}\]
The above equations are linear equations in one variable. Let us find $x$ by eliminating $y$. We multiply 3 with equation (1) and subtract equation (2) from the resulting equation to have;
\[\begin{align}
& 3x+3y-\left( 2x+3y \right)=3-1 \\
& \Rightarrow x=2 \\
\end{align}\]
We put the value of $x=1$ in equation (1) to have the value of $y$as
\[\begin{align}
& \Rightarrow x+y=1 \\
& \Rightarrow 2+y=1 \\
& \Rightarrow y=-1 \\
\end{align}\]
The point of intersection of line (1) and line (2) is $\left( 2,-1 \right)$. We can can express the equation of line as
\[\begin{align}
& x\left( a+2b \right)+y\left( 3a+b \right)=a+b \\
& \Rightarrow xa+2bx-a+3ay+by-b=0 \\
& \Rightarrow a\left( x+y-1 \right)+b\left( 2x+3y-1 \right)=0 \\
& \Rightarrow x+y-1+\dfrac{a}{b}\left( 2x+3y-1 \right)=0 \\
\end{align}\]
The above equation represents the family of lines passing through the point of intersection of $x+y-1=0\Rightarrow x+y=1$ and $2x+3y-1=0\Rightarrow 2x+3y=1$. The point of intersection we obtained as $\left( 2,-1 \right)$. So the correct option is B.\[\]
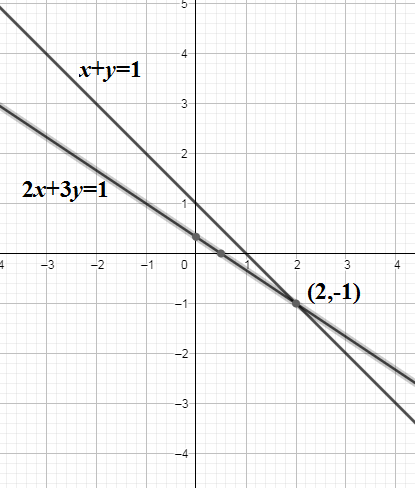
So, the correct answer is “Option B”.
Note: We note that if $L=0$ and ${{L}^{'}}=0$ are two straight lines then the equation of the family of lines that pass through the point of intersection of $L,{{L}^{'}}$ is given with some parameter $\lambda $ as $L+\lambda {{L}^{'}}=0$.The family of lines parallel to $ax+by+c=0$ is given by $ax+by+k=0,k\in R$ and family of lines perpendicular to $ax+by+c=0$ is given by $bx-ay+k=0,k\in R$.
Complete step-by-step answer:
We are given the question that the family of lines $x\left( a+2b \right)+y\left( 3a+b \right)=a+b$ passes through the a fixed point for all values of $a$ and $b$. Let us open the brackets in the left hand side and simplify to
\[\begin{align}
& x\left( a+2b \right)+y\left( 3a+b \right)=a+b \\
& \Rightarrow xa+2bx+3ay+by=a+b \\
\end{align}\]
We take $a$ and $b$ common in the left hand side of the equation in the above step in the above step to have;
\[\Rightarrow a\left( x+y \right)+b\left( 2x+3y \right)=a\cdot 1+b\cdot 1\]
We compare the coefficients of $a,b$ from both side of the question in the above step to have;
\[\begin{align}
& x+y=1.....\left( 1 \right) \\
& 2x+3y=1.....\left( 2 \right) \\
\end{align}\]
The above equations are linear equations in one variable. Let us find $x$ by eliminating $y$. We multiply 3 with equation (1) and subtract equation (2) from the resulting equation to have;
\[\begin{align}
& 3x+3y-\left( 2x+3y \right)=3-1 \\
& \Rightarrow x=2 \\
\end{align}\]
We put the value of $x=1$ in equation (1) to have the value of $y$as
\[\begin{align}
& \Rightarrow x+y=1 \\
& \Rightarrow 2+y=1 \\
& \Rightarrow y=-1 \\
\end{align}\]
The point of intersection of line (1) and line (2) is $\left( 2,-1 \right)$. We can can express the equation of line as
\[\begin{align}
& x\left( a+2b \right)+y\left( 3a+b \right)=a+b \\
& \Rightarrow xa+2bx-a+3ay+by-b=0 \\
& \Rightarrow a\left( x+y-1 \right)+b\left( 2x+3y-1 \right)=0 \\
& \Rightarrow x+y-1+\dfrac{a}{b}\left( 2x+3y-1 \right)=0 \\
\end{align}\]
The above equation represents the family of lines passing through the point of intersection of $x+y-1=0\Rightarrow x+y=1$ and $2x+3y-1=0\Rightarrow 2x+3y=1$. The point of intersection we obtained as $\left( 2,-1 \right)$. So the correct option is B.\[\]
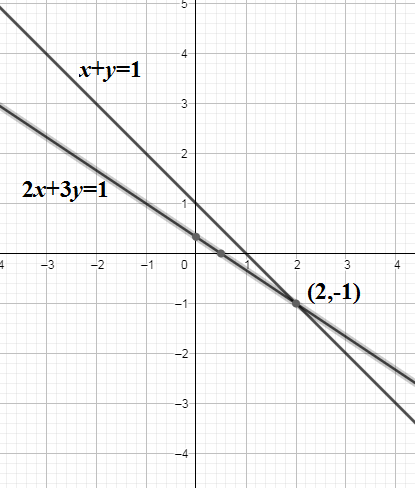
So, the correct answer is “Option B”.
Note: We note that if $L=0$ and ${{L}^{'}}=0$ are two straight lines then the equation of the family of lines that pass through the point of intersection of $L,{{L}^{'}}$ is given with some parameter $\lambda $ as $L+\lambda {{L}^{'}}=0$.The family of lines parallel to $ax+by+c=0$ is given by $ax+by+k=0,k\in R$ and family of lines perpendicular to $ax+by+c=0$ is given by $bx-ay+k=0,k\in R$.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




