Question

If the equation of incircle of an equilateral triangle is ${{x}^{2}}+{{y}^{2}}+4x-6y+4=0$ , then the equation of the circumcircle of the triangle is:
(a) ${{x}^{2}}+{{y}^{2}}+4x+6y-23=0$
(b) ${{x}^{2}}+{{y}^{2}}+4x-6y-23=0$
(c) ${{x}^{2}}+{{y}^{2}}-4x-6y-23=0$
(d) None of these.

Answer 1

Hint: As the given triangle is an equilateral triangle, the incentre and circumcentre coincide, so the centre of the circumcircle and incircle have the same centre, so the equation of the circumcircle and incircle will differ just by the constant term. Therefore, the equation of the circumcircle is ${{x}^{2}}+{{y}^{2}}+4x-6y+c=0$ . Now, we know that $r=4R\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}$ , where r and R are the radius of incircle and circumcircle, respectively.

Complete step-by-step solution -
Let us start by drawing the representative diagram of the situation given in the question.

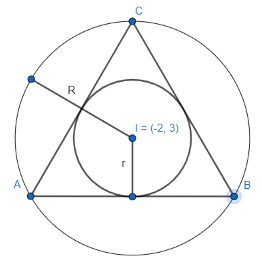
As the given triangle is an equilateral triangle, the incentre and circumcentre coincide, so the centre of the circumcircle and incircle have the same centre, so the equation of the circumcircle and incircle will differ just by the constant term. Therefore, the equation of the circumcircle is ${{x}^{2}}+{{y}^{2}}+4x-6y+c=0$ .
Also, we know that for a circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ , the radius is given by $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ .
$\begin{align}
  & \therefore Inradius=\sqrt{{{2}^{2}}+{{3}^{2}}-4}=3 \\
 & \therefore Circumradius=\sqrt{{{2}^{2}}+{{3}^{2}}-c} \\
\end{align}$
Now we know $r=4R\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}$ , where r and R are the radius of incircle and circumcircle, respectively. Also, as ABC is a equilateral triangle, $\angle A=\angle B=\angle C=60{}^\circ $ .
$r=4R\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}$
$\Rightarrow 3=4\times \left( \sqrt{{{2}^{2}}+{{3}^{2}}-c} \right)\times \sin \dfrac{60{}^\circ }{2}\sin \dfrac{60{}^\circ }{2}\sin \dfrac{60{}^\circ }{2}$
$\Rightarrow 3=4\times \left( \sqrt{{{2}^{2}}+{{3}^{2}}-c} \right)\times {{\sin }^{3}}30{}^\circ $
We know that the value of $\sin 30{}^\circ =\dfrac{1}{2}$ .
$3=4\times \left( \sqrt{{{2}^{2}}+{{3}^{2}}-c} \right)\times {{\left( \dfrac{1}{2} \right)}^{3}}$
$\Rightarrow 6=\sqrt{{{2}^{2}}+{{3}^{2}}-c}$
Now we will square both sides of the equation. On doing so, we get
${{6}^{2}}={{2}^{2}}+{{3}^{2}}-c$
$\Rightarrow 36=4+9-c$
$\Rightarrow c=-23$
So, if we put the value of c in equation of circumcircle, we get
${{x}^{2}}+{{y}^{2}}+4x-6y-23=0$
Therefore, the answer to the above question is option (b).

Note: The key to the above question is knowing the fact that the centre of the circumcentre and the incentre of an equilateral triangle coincide. The other thing you can remember is circumradius of an equilateral triangle is 2 times its inradius. If you want you can directly find the answer by eliminating the option using the fact that the equation of incircle and circumcircle differ by constant term and the circumradius id twice the inradius.