Question

If the earth were to suddenly contract to half its present size, without any change in its mass, the duration of the new day be
A.18 hours
B. 30 hours
C. 6 hours
D. 112 hours

Answer 1

Hint: We know that reduction in Earth’s size implies the reduction in its radius, so, here the radius is reduced to half. Find the moment of inertia of earth before and after contraction keeping in mind that the mass remains constant. Now, you could substitute them and the expression of angular velocities before and after contraction in the law of conservation of angular momentum and thus get the time period of one rotation of earth, that is, the duration of a day.

Formula used:
Moment of inertia of a solid sphere,
$I=\dfrac{2}{5}M{{R}^{2}}$
Expression for angular velocity,
$\omega =\dfrac{2\pi }{T}$
Law of conservation of angular momentum,
${{I}_{1}}{{\omega }_{1}}={{I}_{2}}{{\omega }_{2}}$

Complete step-by-step answer:

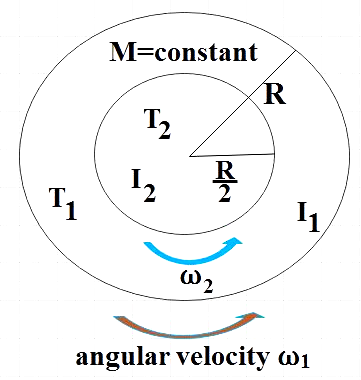
We are given that the Earth is contracted to half its present size. Change in size implies change in radius, so, here the present radius of earth $\left( {{R}_{1}} \right)$ is reduced by half. That is, after contraction the radius becomes,
${{R}_{2}}=\dfrac{{{R}_{1}}}{2}$ ………………………………. (1)
But during the contraction, the mass remains constant. That is,
${{M}_{1}}={{M}_{2}}=M$ ……………………………… (2)
Due to the above mentioned contraction, the angular velocity of Earth’s rotation changes. Also, we know that angular velocity is given by,
$\omega =\dfrac{2\pi }{T}$
Angular velocity before contraction,
$\Rightarrow {{\omega }_{1}}=\dfrac{2\pi }{{{T}_{1}}}$ ………………………… (3)
Angular velocity after contraction,
$\Rightarrow {{\omega }_{2}}=\dfrac{2\pi }{{{T}_{2}}}$ ……………………………….. (4)
There is another quantity that is undergoing change due to contraction of earth – moment of inertia.
Moment of inertia of a solid sphere is given by,
$I=\dfrac{2}{5}M{{R}^{2}}$
Moment of inertia before contraction,
${{I}_{1}}=\dfrac{2}{5}M{{R}_{1}}^{2}$ …………………………. (5)
Moment of inertia after contraction,
${{I}_{2}}=\dfrac{2}{5}M{{R}_{2}}^{2}=\dfrac{2}{5}M{{\left( \dfrac{{{R}_{1}}}{2} \right)}^{2}}=\dfrac{{{I}_{1}}}{4}$ ………………………………. (6)
Now, by the law of conservation of angular momentum,
$\dfrac{dL}{dt}=0$
$\Rightarrow L=I\omega $= constant
$\Rightarrow {{I}_{1}}{{\omega }_{1}}={{I}_{2}}{{\omega }_{2}}$ …………………………….. (7)
Substituting (3), (4) and (6) in (7), we get,
${{I}_{1}}\left( \dfrac{2\pi }{{{T}_{1}}} \right)=\left( \dfrac{{{I}_{1}}}{4} \right)\left( \dfrac{2\pi }{{{T}_{2}}} \right)$
$\Rightarrow {{T}_{2}}=\dfrac{{{T}_{1}}}{4}$ ………………….. (8)
But we know the present time period rotation of our planet Earth as 24 hours. Therefore,
${{T}_{1}}=24Hrs$ …………… (9)
 Substituting (9) in equation (8), we get,
${{T}_{2}}=\dfrac{24}{4}$
$\Rightarrow {{T}_{2}}=6Hrs$
Time period of rotation of Earth is what we call a day. So, for an Earth that is contracted to half its present size with mass constant, the duration of a day will be just 6hrs.

So, the correct answer is “Option C”.

Note: Though we have discussed the case where the size of the Earth is reduced by half, we could actually generalize the above relation. Let us consider that Earth is contracted to $\dfrac{1}{n}th$ of its present size,
$\Rightarrow {{R}_{2}}=\dfrac{{{R}_{1}}}{n}$
$\Rightarrow {{I}_{2}}=\dfrac{2}{5}M{{\left( \dfrac{{{R}_{1}}}{n} \right)}^{2}}=\dfrac{{{I}_{1}}}{{{n}^{2}}}$
Substituting in (7) and then rearranging,
${{T}_{2}}=\dfrac{{{T}_{1}}}{{{n}^{2}}}=\dfrac{24}{{{n}^{2}}}$
This generalization is under the condition that the mass of earth remains constant.