Question

If the distance between two parallel tangents is $ 14 $ cm. find its radius.

Answer 1

Hint: Tangent is the line to a circle which touches the circle exactly at the one point. Tangent of the circle never intersects the circle. Here we will construct the diagram with the help of the given conditions and will find the radius.

Complete step-by-step answer:
First draw two tangents of the circle using the property so tangents are always perpendicular to the radius of the circle.

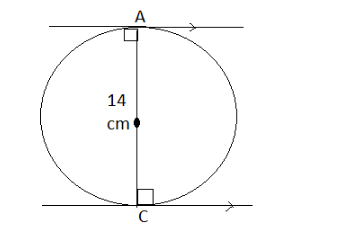
Let us assume that the tangent touches the circle at the point “A” and the point “C” making the right angles.
Now, the line-segment AC will be the straight line because the alternative intersecting angles are equal.
So, the given measure is twice the radius.
 $ \therefore r + r = 14cm $
Simplify the above equation- like terms are directly added on the left hand side of the equation.
 $ \Rightarrow 2r = 14 $
When the term is in the multiplicative with the other term at one side changes its side goes to the division on the opposite side and vice versa.
 $ \Rightarrow r = \dfrac{{14}}{2} $
Take common multiple and remove them from the numerator and the denominator.
 $ \Rightarrow r = 7cm $
Hence, the required answer – the radius is $ 7cm $

Note: Also, refer to the tangent-secant theorem and all its concepts for the easy application for an accurate and efficient solution. These types of questions solely depend on the properties, so remember them by heart.
The point at which the tangent touches the circle is known as the point of the tangency. The tangent of the circle is always perpendicular to the radius of the point of the tangency.