Question

If the differential equation representing the family of all circles touching x-axis at the origin is \[\left( {{x^2} - {y^2}} \right)\dfrac{{dy}}{{dx}} = g\left( x \right)y\] , then \[g\left( x \right)\] equals
(A) \[\dfrac{1}{2}x\]
(B) \[2{x^2}\]
(C) \[2x\]
(D) \[\dfrac{1}{2}{x^2}\]

Answer 1

Hint: Here we will first write the general equation for family of circles x-axis at the origin and then differentiate it with respect to x and then compare the resulting equation with the given equation to get the value of \[g\left( x \right)\]

Complete step-by-step answer:
The general equation for family of circles x-axis at the origin is given by:-
\[{\left( {x - 0} \right)^2} + {\left( {y - a} \right)^2} = {a^2}\] with center at \[\left( {0,a} \right)\] and radius equal to \[a\]
               

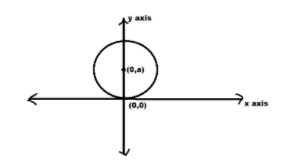
Simplifying the above equation we get:-
\[{\left( x \right)^2} + {\left( {y - a} \right)^2} = {a^2}\]…………………………………………(1)
Differentiating the above equation with respect to x we get:-
We will use the following formula of differentiation:-
\[\dfrac{d}{{dx}}\left( {{x^n}} \right) = n{x^{n - 1}}\]
Also, the derivative of a constant is zero.
Applying this formula we get:-
\[2{x^1} + 2{\left( {y - a} \right)^1}\dfrac{{dy}}{{dx}} = 0\]
Simplifying it further we get:-
\[2x + 2\left( {y - a} \right)\dfrac{{dy}}{{dx}} = 0\]
Taking 2 as common we get:-
\[
  2\left[ {x + \left( {y - a} \right)\dfrac{{dy}}{{dx}}} \right] = 0 \\
   \Rightarrow x + \left( {y - a} \right)\dfrac{{dy}}{{dx}} = 0 \\
 \]
Now we will evaluate the value of a:
Hence on evaluating we get:-
\[
  x + y\dfrac{{dy}}{{dx}} - a\dfrac{{dy}}{{dx}} = 0 \\
   \Rightarrow a\dfrac{{dy}}{{dx}} = x + y\dfrac{{dy}}{{dx}} \\
 \]
Simplifying it further we get:-
\[a = \dfrac{x}{{\dfrac{{dy}}{{dx}}}} + y\]……………………………(2)
Now simplifying equation 1 we get:-
We will use the following identity:-
\[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\]
Hence applying this identity we get:-
\[{x^2} + \left[ {{y^2} + {a^2} - 2ay} \right] = {a^2}\]
Simplifying it further we get:-
\[{x^2} + {y^2} - 2ay = 0\]
Now putting the value of equation 2 in the above equation we get:-
\[{x^2} + {y^2} - 2\left( {\dfrac{x}{{\dfrac{{dy}}{{dx}}}} + y} \right)y = 0\]
Simplifying it further we get:-
\[
  {x^2} + {y^2} - 2y\left( {\dfrac{x}{{\dfrac{{dy}}{{dx}}}}} \right) - 2{y^2} = 0 \\
   \Rightarrow {x^2} - {y^2} - 2y\left( {\dfrac{x}{{\dfrac{{dy}}{{dx}}}}} \right) = 0 \\
 \]
Now taking LCM we get:-
\[\dfrac{{\left( {{x^2} - {y^2}} \right)\dfrac{{dy}}{{dx}} - 2xy}}{{\dfrac{{dy}}{{dx}}}} = 0\]
Now on cross multiplying we get:-
\[
  \left( {{x^2} - {y^2}} \right)\dfrac{{dy}}{{dx}} - 2xy = 0 \\
   \Rightarrow \left( {{x^2} - {y^2}} \right)\dfrac{{dy}}{{dx}} = 2xy \\
 \]
Now comparing this equation with the given equation i.e. \[\left( {{x^2} - {y^2}} \right)\dfrac{{dy}}{{dx}} = g\left( x \right)y\]
We get:-
\[g\left( x \right) = 2x\]

So, the correct answer is “Option C”.

Note: Students might make mistake in forming the equation of the family of circles touching the x-axis at the origin and also while differentiating the terms so all the steps should be carefully followed. Also, students should take care of calculations in order to get the correct answer.