Question

If the diagonals of a rhombus are equal, then the rhombus is a
A) Parallelogram but not a square
B) Parallelogram but not rectangle
C) Rectangle but not a square
D) Square

Answer 1

Hint: Draw the figure of the required shape and try to grab what's already given in the question or what you can observe from the figure and try to prove that all the angles of the rhombus are equal i.e., \[{90^ \circ }\] .
Complete step by step answer:
Let's try to draw a rhombus first with the given property illustrated in the question.

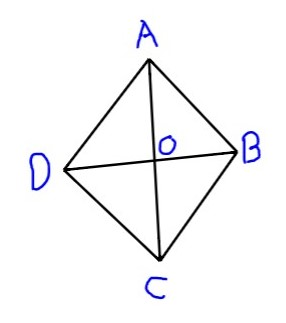
Here ABCD is a rhombus and AC and DB are the equal diagonals
We know that the diagonals of a rhombus bisect each other.
As it is given that \[AC = BD\] Therefore clearly we can write that
\[OA = OB = OC = OD\]
Now let us consider \[\vartriangle AOB\]
\[ \Rightarrow OA = OB\& \angle AOD = {90^ \circ }\]
 \[\angle OAB\& \angle OBA\] must be equal Therefore by the properties of triangle we know that sum of all angles of a triangle must be \[{180^ \circ }\] using this property we can write that
\[\angle OAB + \angle OBA + \angle AOB = {180^ \circ }\] it is also known that \[\angle AOB = {90^ \circ }\]
\[\begin{array}{l}
\therefore \angle OAB + \angle OBA = {90^ \circ }\\
 \Rightarrow 2\angle OAB = {90^ \circ }\\
 \Rightarrow \angle OAB = \dfrac{{{{90}^ \circ }}}{2} = {45^ \circ }\\
\therefore \angle OBA = \angle OAB = {45^ \circ }
\end{array}\]
Similarly in \[\vartriangle AOD\]
\[\begin{array}{l}
 \Rightarrow \angle OAD = \angle ODA = {45^ \circ }\\
\therefore \angle DAB = \angle OAB + \angle OAD = {45^ \circ } + {45^ \circ } = {90^ \circ }\\
\end{array}\]
Similarly,
\[\begin{array}{l}
 \Rightarrow \angle ABC = \angle BCD = \angle CDA = {90^\circ }\\
here, AB = BC = CD = DA \\
\end{array}\]
Now clearly rhombus ABCD is a square. Option D is correct.

Note: This question can also be approached in a different manner we can try to prove that \[\vartriangle AOB \cong \vartriangle BOC \cong \vartriangle COD \cong \vartriangle DOA\] which means all of this triangles are congruent to each other and that again itself proves \[AB = BC = CD = DA\] which again means that the given rhombus is a square.