Question

If the diagonals of a quadrilateral bisect each other , then it is a parallelogram .

Answer 1

Hint: Let us suppose the quadrilateral ABCD with diagonal bisect at point O . So first let us prove that the triangle AOD and triangle COB is congruent and triangle DOC and triangle BOA is congruent by the SAS congruence rule . So from this Angle OAD and Angle OCB are alternate angles and are equal and Angle ABO and Angle CDO are alternate angles and are equal using this we can prove this

Complete step-by-step answer:

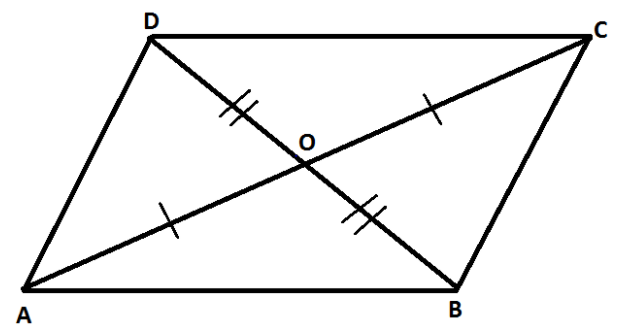
As it is given that the ABCD is an quadrilateral with it diagonal AC and BD which intersect at the point O , and It is also given that the diagonal bisect each other , that is
OA=OC and OB=OD
In triangle AOD and COB
 OA=OC It is given in the question
 Angle AOD = Angle COB because it is vertical opposite
 OD=OB It is given in the question
Hence the triangle AOD and triangle COB is congruent by the SAS congruence rule .
So from this we can say that angle OAD = angle OCB
Similarly, we for triangle AOB and the triangle COD
OD=OB It is given in the question
 Angle DOC = Angle BOA because it is vertical opposite
 OA = OC It is given in the question
 Hence the triangle DOC and triangle BOA is congruent by the SAS congruence rule .
So from this we can say that angle ODC = angle OBA
 For lines AB and CD and the transversal line BD,
 Angle ABO and Angle CDO are alternate angles and are equal.
hence both Lines are parallel ${\text{AB}}\left\| {{\text{CD}}} \right.$
For lines AD and BC, and the transversal line AC,
Angle OAD and Angle OCB are alternate angles and are equal.
hence both Lines are parallel ${\text{AD}}\left\| {{\text{BC}}} \right.$
Thus, in quadrilateral ABCD, both pairs of opposite sides are parallel.
Hence ABCD is a parallelogram.

Note: There are five ways to find out that two triangles are congruent are SSS, SAS, ASA, AAS and HL ( hypotenuse ,leg
ABC is a right-angled triangle and O is the midpoint of the side opposite to the right angle then O is equidistant from A, B, and C