Question

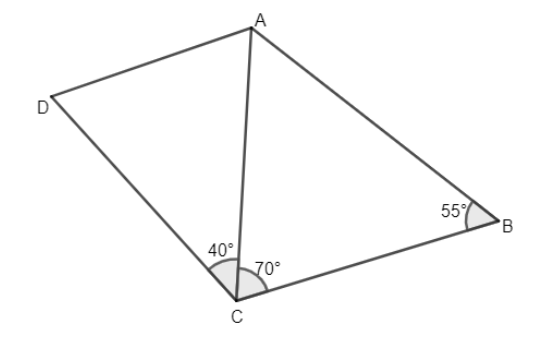
If the \[\text{DA}=\text{CB}\] , what is the measure of \[\angle \text{DAC}\] ?

A. \[{{70}^{\circ }}\]
B. \[{{100}^{\circ }}\]
C. \[{{95}^{\circ }}\]
D. \[{{125}^{\circ }}\]

Answer 1

Hint: Here, in this problem first of all we need to understand the concept and property of isosceles triangles. First, we have to use the property of triangle in \[\Delta ABC\] to find the angle \[\angle A\] then we have to use the property of isosceles triangle in \[\Delta ACD\] to find the angle \[\angle D\] then again using the property of triangle \[\Delta ACD\] to find the angle \[\angle A\] .

Complete step by step solution:
Before we go to the problem, first of all we need to understand the concept of Isosceles triangle and also the property of the triangle.
Isosceles triangle is the triangle in which two sides are always equal and in equilateral triangle three sides are equal.
Some important property of triangle:
The two angles of an isosceles triangle which are opposite to two equal sides are also considered to be equal.
Two sides of an isosceles triangle which are opposite to the equal are also considered to be equal.
Angle property of a triangle is the sum of all angles of a triangle which is equal to \[{{180}^{\circ }}\] .
Above mentioned, the property of the triangle will be required to solve this type of problem.
Now, we come to the problem,
In this type of the problem given that \[\text{DA}=\text{CB}\] we have to measure the \[\angle \text{DAC}\] that means we have to measure the \[\angle A\] in the \[\Delta ACD\].
For that we have to use the \[\Delta ABC\]
Given that \[\text{DA}=\text{CB}\]
In \[\Delta ABC\] ,
We have to use the angle property of a triangle that is the sum of all angles equal to \[{{180}^{\circ }}\] .
 \[\angle A + \angle B + \angle C={{180}^{\circ }}---(1)\]
According to the given figure, \[\angle B={{55}^{\circ }}\] and \[\angle C={{70}^{\circ }}\] . Substitute these values on equation (1) we get:
 \[\angle A+{{55}^{\circ }}+{{70}^{\circ }}={{180}^{\circ }}\]
After simplifying this we get:
 \[\angle A={{180}^{\circ }}-{{55}^{\circ }}-{{70}^{\circ }}\]
Further solving this we get:
 \[\angle A={{55}^{\circ }}\]
As we know that \[\text{DA}=BC--(2)\] but by using the property of isosceles triangle we can also say that \[\text{AC}=BC--(3)\] by equation (1) and equation (2) we get:
 \[DA=AC=BC\]
In \[\Delta ACD\]
By using the property of a triangle that is isosceles, triangle angles opposite to equal sides are always equal.
That means \[\angle D=\angle C={{40}^{\circ }}\]
 \[\angle A+\angle D+\angle C={{180}^{\circ }}---(4)\]
Substitute the value of \[\angle D={{40}^{\circ }}\] as well as \[\angle C={{40}^{\circ }}\] on equation (4) we get:
 \[\angle A+{{40}^{\circ }}+{{40}^{\circ }}={{180}^{\circ }}\]
By simplifying this we get:
 \[\angle A={{180}^{\circ }}-{{40}^{\circ }}-{{40}^{\circ }}\]
Further solving we get:
 \[\angle A={{100}^{\circ }}\]
 \[\therefore \Delta DAC={{100}^{\circ }}\]
So, the correct option is “option B”.
So, the correct answer is “Option B”.

Note: To solve this type of problem, we have to remember the property of triangles and also isosceles triangles. Angle property of the triangle is very important in this problem. Most of students may mistake while finding the angles \[\angle A\] they will calculate in the triangle \[\Delta ABC\] and end up with the answer that is wrong because, in this question, we have to find the angle \[\angle A\] in the \[\Delta \text{ADC}\] . So, students have to read the question carefully which angle is asked in the triangle to avoid mistakes in the exam.