Question

If the cardinality of set A is $4$ and that of a set B is $3$ then what is the cardinality of the set $A\Delta B$.
A. $1$
B. $5$
C. $7$
D. Cannot be determined

Answer 1

Hint: Here we need to know what $A\Delta B$ means. It refers to all the elements that are there in the set A or the set B but not in their intersection or we can say that all the elements that are there in either set A or set B nut we don’t need to include the elements common to both the set A and B.

Complete Step by Step Solution:
Here we are given that the cardinality of set A is $4$ and that of a set B is $3$.
We must know the meaning of cardinality. It is actually the number of elements that are there in the set. As here we are given that the cardinality of set A is $4$ and that of a set B is $3$ this means that there are $4$ elements in the set A and there are $3$ elements in the set B.
So we can write it as:
$
  n\left( A \right) = 4 \\
  n\left( B \right) = 3 \\
 $
So we need to find the cardinality of $A\Delta B$ set.
Let us see through Venn diagram that:

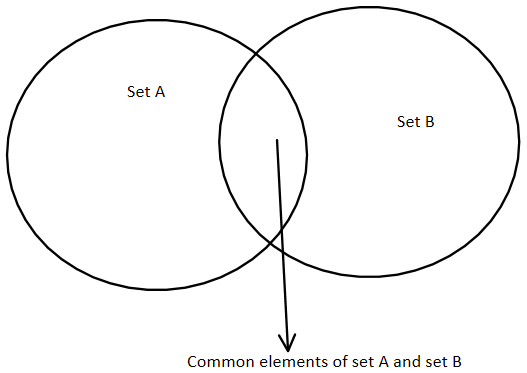
We know that $A\Delta B$ means all the elements that are there in the set A or the set B but not in their intersection or we can say that all the elements that are there in either set A or set B nut we don’t need to include the elements common to both the set A and B.
We can write that:
$n\left( {A\Delta B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)$
Here we know the values of $n\left( A \right){\text{ and }}n\left( B \right)$ but not the elements that are common to ${\text{A and B}}$.
Hence we do not know what $n\left( {A \cap B} \right)$ is. Therefore the value of $n\left( {A\Delta B} \right)$ cannot be determined.

Hence we can say that D) is the correct option.

Note:
Here in these types of problems we must know all the symbols that are used in the sets related problems. If we are given the set $\left( {B - A} \right)$ then this would mean that all the elements that are there in set B but not in the set A. These problems can be easily solved by using the Venn diagram.