Question

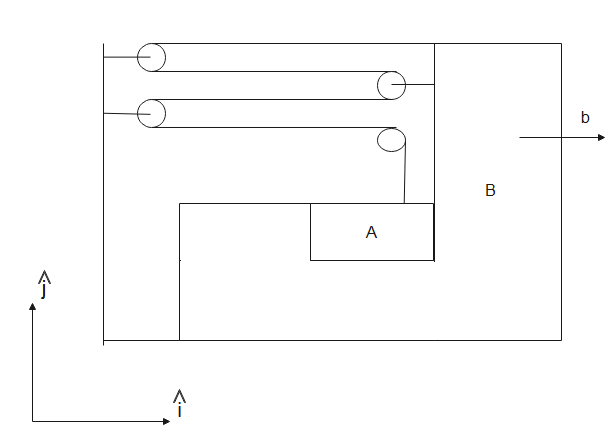
If the block B moves towards right with acceleration\[b\], the net acceleration of block A is-
(A). \[b\hat{i}+4b\hat{j}\]
(B). \[b\hat{i}+b\hat{j}\]
(C). \[b\hat{i}+2b\hat{j}\]
(D). None of these

Answer 1

Hint: Resolve the figure into its component systems. Solve for each system by computing the forces acting on each system and then use it to calculate acceleration. For acceleration in the x-direction, use all the forces acting along the x-axis. For acceleration along the y-direction, use all forces along the y-axis.


Complete step by step answer:
The block B is moving with acceleration \[b\]in the x-direction.
As we can see from the fig, block A is a part of the system of block B, so it will also move with \[b\]acceleration along the x-axis.
Therefore, \[x=b\hat{i}\] - (1)

 

When block B moves\[x\]distance in the x-direction, string over each pulley moves\[x\]distance due to which the block A moves\[4x\]distance in the y-direction. Therefore, we can say that,
\[\begin{align}
  & y=4x \\
 & \dfrac{dy}{dt}=4\dfrac{dx}{dt} \\
 & \Rightarrow \dfrac{{{d}^{2}}y}{d{{t}^{2}}}=4\dfrac{{{d}^{2}}x}{d{{t}^{2}}} \\
\end{align}\]
\[\therefore a=4b\] - (2)
 Here, \[a\]is the acceleration in the y-direction. Therefore, acceleration in terms of its components from eq (1) and eq (2) will be-
\[a'=b\hat{i}+4b\hat{j}\]
Acceleration of block A is given by\[a'=b\hat{i}+4b\hat{j}\].

So, the correct answer is “Option A”.

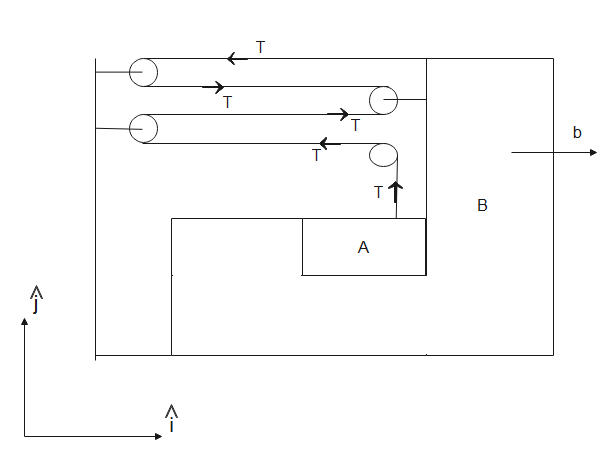
Additional Information: The pulling or stretching force acting in a string is called tension. It is denoted by \[T\].

Note: The pulleys are assumed to be in rest. The tension in the string is equal across the pulleys as long as there is no component attached to the string. The relationship between force and acceleration is given by Newton’s second law of motion which states that acceleration of a body is directly proportional to the force applied and inversely proportional to its mass.