Question

If the bisectors of a pair of corresponding angles formed by transversal are parallel, then prove that given lines are parallel.

Answer 1

Hint: First, we will draw a figure using the data given to us. Then we should know that if the angle bisector is drawn then the angle is equally divided into equal measures. Further, we will use the concept of corresponding angles axiom i.e. given as: if a transversal intersects two parallel lines such that a pair of corresponding angles is equal then the two lines are parallel. Using this we will prove that given lines are parallel.

Complete step-by-step solution -

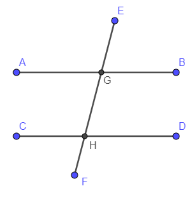
Here, we are given that two straight lines are cut by transversal at some random points. So, the diagram is as shown below.

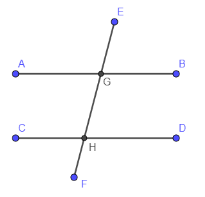
Here, AB and CD are two straight lines. EF is transversal which cuts lines at point G and H. Now, we will draw bisector GI and HJ of corresponding angles $\angle EGB$ and $\angle GHD$ such that $GI\parallel HJ$ .

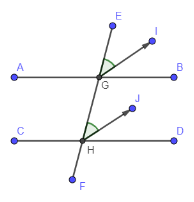
Therefore, here $\angle EGI=\angle GHJ$ . This is called corresponding angles. Now, we can write $\angle EGB$ as addition of two angles i.e. $\angle EGI+\angle IGB$ . Here, as GI is bisector so we can say that angle EGI and IGB are equal i.e. $\angle EGI=\angle IGB$ . So, we can say that $\angle EGB=\angle EGI+\angle EGI=2\angle EGI$ .
In the same way, we can write $\angle GHD$ as addition of two angles i.e. $\angle GHJ+\angle JHD$ . Here, as HJ is bisector so we can say that angle GHJ and JHD are equal i.e. $\angle GHJ=\angle JHD$ . So, we can say that $\angle GHD=\angle GHJ+\angle GHJ=2\angle GHJ$ .
Here, using the corresponding angles axiom we can say that: if a transversal intersects two parallel lines such that a pair of corresponding angles is equal then the two lines are parallel.
Thus, using the corresponding angles axiom, we can say that corresponding angle is equal i.e. $\angle EGB=\angle GHD$. So, lines AB and CD are said to be parallel.

Note: This is a theory-based question, so here some basic concepts like angle bisector and corresponding angle axiom should be very clear. Also, students should know the difference between corresponding angle and alternate angles. In this case, alternate angles are $\angle BGH$ and $\angle GHC$ . So, do not get confused in alternate and corresponding angles.