Question

If the below equation is balanced with lowest whole number coefficients, find the coefficient for \[{H^ + }\] (aq).
\[Cu\left( s \right){\text{ }} + {\text{ }}N{O_3}^ - \left( {aq} \right){\text{ }} + {\text{ }}{H^ + }\left( {aq} \right) \to {\text{ }}C{u^{2 + }}\left( {aq} \right){\text{ }} + {\text{ }}N{O_2}\left( g \right){\text{ }} + {\text{ }}{H_2}O\left( l \right)\]
\[
  A.\;\;\;\;\;1 \\
  B.\;\;\;\;\;2 \\
  C.\;\;\;\;\;3 \\
  D.\;\;\;\;\;4 \\
  E.\;\;\;\;\;\;5 \\
 \]

Answer 1

Hint: For this question one should know the oxidation states of the atom. If you don’t know the oxidation state directly then you should know how to find out the oxidation state of any atom. Make sure every atom on both sides is equal in number.

Complete answer: The equation given to us is:
\[Cu\left( s \right){\text{ }} + {\text{ }}N{O_3}^ - \left( {aq} \right){\text{ }} + {\text{ }}{H^ + }\left( {aq} \right) \to {\text{ }}C{u^{2 + }}\left( {aq} \right){\text{ }} + {\text{ }}N{O_2}\left( g \right){\text{ }} + {\text{ }}{H_2}O\left( l \right)\]
This equation is an unbalanced equation. For balancing it first we will assign oxidation numbers to all the atoms.
\[\mathop {Cu}\limits^0 \left( s \right){\text{ }} + {\text{ }}\mathop N\limits^{ + 5} {O_3}^ - \left( {aq} \right){\text{ }} + {\text{ }}{H^ + }\left( {aq} \right) \to {\text{ }}\mathop {C{u^{2 + }}}\limits^{ + 2} \left( {aq} \right){\text{ }} + {\text{ }}\mathop N\limits^{ + 4} {O_2}\left( g \right){\text{ }} + {\text{ }}{H_2}O\left( l \right)\]
This can also be written as:

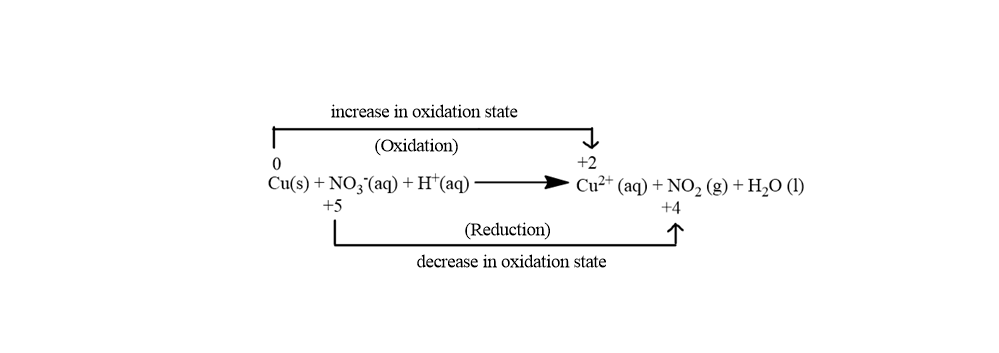
In the above image, we see that there is an increase in the oxidation number of Cu from $0$ to $ + 2$ and there is a decrease in the oxidation number of N from $ + 5$ to $ + 4$
So in the reaction, the total increase in the oxidation state is $2$ and the total decrease in the oxidation state is $1$. Now we need to balance the increase in oxidation state with the decrease in the oxidation state so for balancing this we will just multiply Cu with $1$ and multiply N with $2$. Multiplication will take place in the following manner:
\[(Cu(s) \to C{u^{2 + }}) \times 1\]
\[(N{O_3}^ - \to N{O_2}) \times 2\]
After multiplying, the reaction will be as follows:
\[Cu\left( s \right){\text{ }} + {\text{ 2}}N{O_3}^ - \left( {aq} \right){\text{ }} + {\text{ }}{H^ + }\left( {aq} \right) \to {\text{ }}C{u^{2 + }}\left( {aq} \right){\text{ }} + {\text{ 2}}N{O_2}\left( g \right){\text{ }} + {\text{ }}{H_2}O\left( l \right)\]
Now we see in the above reaction that our Cu and N species are completely balance so now we look onto H and O. on the left hand side we see that $6$ O atoms are present and on the right hand side only $5$ are present so we will add another molecule of $H_2O$ to balance O on both the side. After balancing the reaction is as follows:
\[Cu\left( s \right){\text{ }} + {\text{ 2}}N{O_3}^ - \left( {aq} \right){\text{ }} + {\text{ }}{H^ + }\left( {aq} \right) \to {\text{ }}C{u^{2 + }}\left( {aq} \right){\text{ }} + {\text{ 2}}N{O_2}\left( g \right){\text{ }} + {\text{ 2}}{H_2}O\left( l \right)\]
Lastly the only species left to balance is \[{H^ + }\] atoms so to balance this we will just add $3$ more protons or \[{H^ + }\] atoms on the left hand side. Thus the final reaction comes to be:
\[Cu\left( s \right){\text{ }} + {\text{ 2}}N{O_3}^ - \left( {aq} \right){\text{ }} + {\text{ 4}}{H^ + }\left( {aq} \right) \to {\text{ }}C{u^{2 + }}\left( {aq} \right){\text{ }} + {\text{ 2}}N{O_2}\left( g \right){\text{ }} + {\text{ 2}}{H_2}O\left( l \right)\]
Hence the above equation is balanced and the coefficient of \[{H^ + }\] is \[4\].
Therefore the correct option is D.

Note:
While balancing the chemical equation we apply the law of conservation of mass which states that the mass of the products in a chemical reaction must equal the mass of the reactants.