Question

If the axes are rotated through an angle of \[30^\circ \] in the clockwise direction, the point \[\left( {4,2\sqrt 3 } \right)\] in the new system is
\[{\text{A) }}\left( {2,3} \right)\]
\[{\text{B) }}\left( {2,\sqrt 3 } \right)\]
\[{\text{C) }}\left( {\sqrt 3 ,2} \right)\]
\[{\text{D) }}\left( {\sqrt 3 ,5} \right)\]

Answer 1

Hint: Let the point in the new system is given by (X,Y) where \[{\text{X = xcos}}\theta {\text{ + ysin}}\theta \] and \[{\text{Y = - xsin}}\theta {\text{ + ycos}}\theta \] .We can easily calculate the values of X and Y because the values of x, y and theta is given to us in the question. We take theta as negative because the axes are rotated in the clockwise direction. By solving it further we will get the point in the new system.

Complete step-by-step solution:

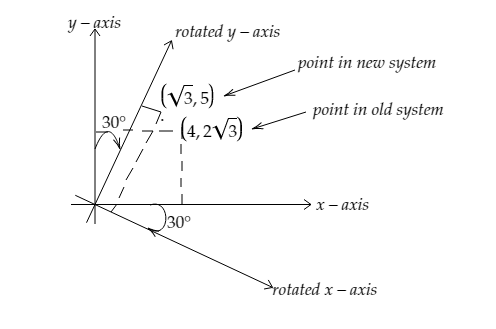
Rotation consists of rotating the object around the point \[\left( {0,0} \right)\]. Then the clockwise rotation of the point (x,y) into the point (X,Y) by the angle \[\theta \] about \[\left( {0,0} \right)\] is expressed by
\[{\text{X = xcos}}\theta {\text{ + ysin}}\theta \] ----------- (i)
 and \[{\text{Y = - xsin}}\theta {\text{ + ycos}}\theta \] ------------ (ii)
It is given to us that the axes are rotated through an angle of \[30^\circ \] in the clockwise direction therefore \[\theta = - 30^\circ \]. Also the point given to us is \[\left( {4,2\sqrt 3 } \right)\] .So we can say that \[{\text{x = 4}}\] and \[{\text{y = 2}}\sqrt 3 \] .
By putting these values in equations (i) and (ii) we get
\[\left( i \right) \Rightarrow {\text{ X = 4cos30}}^\circ - {\text{2}}\sqrt 3 \sin 30^\circ \]
We know that the value of \[{\text{cos30}}^\circ \] is \[\dfrac{{\sqrt 3 }}{2}\] and the value of \[\sin 30^\circ \] is \[\dfrac{1}{2}\] .Therefore, the above expression becomes
\[ \Rightarrow {\text{ X = 4}}\left( {\dfrac{{\sqrt 3 }}{2}} \right) - {\text{2}}\sqrt 3 \left( {\dfrac{1}{2}} \right)\]
On dividing the numerator by \[2\] we get
\[ \Rightarrow {\text{ X = 2}}\sqrt 3 - \sqrt 3 \]
By adding both the terms we get
\[ \Rightarrow {\text{ X = }}\sqrt 3 \]
Similarly, the equation will be
\[\left( {ii} \right) {\text{ Y = }}4{\text{sin30}}^\circ {\text{ + 2}}\sqrt 3 {\text{cos30}}^\circ \]
As we know that the value of \[{\text{sin30}}^\circ \] is \[\dfrac{1}{2}\] and the value of \[{\text{cos30}}^\circ \] is \[\dfrac{{\sqrt 3 }}{2}\] .So by putting these values in the above expression we get
\[ \Rightarrow {\text{ Y = }}4\left( {\dfrac{1}{2}} \right){\text{ + 2}}\sqrt 3 \left( {\dfrac{{\sqrt 3 }}{2}} \right)\]
On dividing the numerators by their denominators we get
\[ \Rightarrow {\text{ Y = }}2{\text{ + 3}}\]
By doing addition we get
\[ \Rightarrow {\text{ Y = 5}}\]
Therefore the point in the new system is \[\left( {\sqrt 3 ,5} \right)\] .
Hence the correct option is \[{\text{D) }}\left( {\sqrt 3 ,5} \right)\]

Note: Keep in mind that $cos(-\theta) = cos(\theta)$ and $sin(-\theta) = - sin(\theta)$. Note that counterclockwise is the positive rotation direction and clockwise is the negative direction. Remember all the trigonometric values.