
If the area of the triangle formed by the points ( x , 2x ), ( -2 ,6) and ( 3,1) is 5 sq.units then x is
a.$\dfrac{2}{3}$
b.$\dfrac{3}{5}$
c.3
d.5
Answer
586.8k+ views
Hint: with the given coordinates we know that the formula of area of the triangle is $\dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]$ substituting the given formula in this and equating it to 5 we get the value of x.
Complete step-by-step answer:
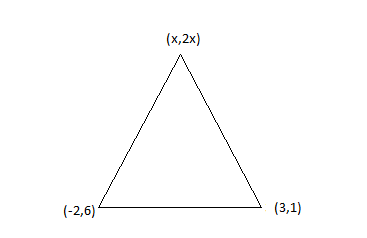
We are given the coordinates of the vertices of the triangle
$
\Rightarrow A({x_1},{y_1}) = (x,2x) \\
\Rightarrow B({x_2},{y_2}) = ( - 2,6) \\
\Rightarrow C({x_3},{y_3}) = (3,1) \\
$
We know that the area of a triangle is given by
$ \Rightarrow \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]$
And we are given that the area is 5 sq units
$ \Rightarrow \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right] = 5sq.units$
Substituting the given points we get
$
\Rightarrow \dfrac{1}{2}\left[ {x\left( {6 - 1} \right) - 2\left( {1 - 2x} \right) + 3\left( {2x - 6} \right)} \right] = 5sq.units \\
\Rightarrow \dfrac{1}{2}\left[ {6x - x - 2 + 4x + 6x - 18} \right] = 5sq.units \\
\Rightarrow \dfrac{1}{2}\left[ {15x - 20} \right] = 5sq.units \\
\Rightarrow 15x - 20 = 10 \\
\Rightarrow 15x = 30 \\
\Rightarrow x = \dfrac{{30}}{{15}} = 2 \\
$
Hence we get the value of x to be 2
None of the options match the answer.
Note: By finding the product of a point's x coordinate times the next point's y coordinate, then subtracting the y coordinate of the first point times the x coordinate of the second coordinate and dividing by two, you will find the area of the polygon.
Complete step-by-step answer:
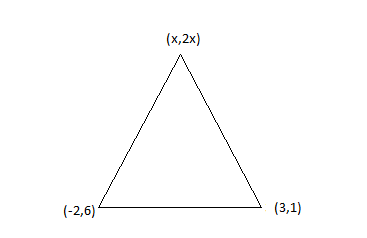
We are given the coordinates of the vertices of the triangle
$
\Rightarrow A({x_1},{y_1}) = (x,2x) \\
\Rightarrow B({x_2},{y_2}) = ( - 2,6) \\
\Rightarrow C({x_3},{y_3}) = (3,1) \\
$
We know that the area of a triangle is given by
$ \Rightarrow \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]$
And we are given that the area is 5 sq units
$ \Rightarrow \dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right] = 5sq.units$
Substituting the given points we get
$
\Rightarrow \dfrac{1}{2}\left[ {x\left( {6 - 1} \right) - 2\left( {1 - 2x} \right) + 3\left( {2x - 6} \right)} \right] = 5sq.units \\
\Rightarrow \dfrac{1}{2}\left[ {6x - x - 2 + 4x + 6x - 18} \right] = 5sq.units \\
\Rightarrow \dfrac{1}{2}\left[ {15x - 20} \right] = 5sq.units \\
\Rightarrow 15x - 20 = 10 \\
\Rightarrow 15x = 30 \\
\Rightarrow x = \dfrac{{30}}{{15}} = 2 \\
$
Hence we get the value of x to be 2
None of the options match the answer.
Note: By finding the product of a point's x coordinate times the next point's y coordinate, then subtracting the y coordinate of the first point times the x coordinate of the second coordinate and dividing by two, you will find the area of the polygon.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




