Question

If the area of the rhombus enclosed by the lines \[lx\pm my\pm n=0\] be 2 sq. units, then
A). l, m, n are in G.P
B). l, n, m are in G.P
C). lm = n
D). ln = m

Answer 1

Hint: Draw the diagram and find the points of intersection of four lines. Points of intersections are calculated by taking two lines at a time and then solve the two equations. For instance, let us take two lines $lx+my-n=0; lx-my+n=0$. Now, to solve these two equations we will add them then variable y will be eliminated and we are left with x and then solve x. After getting the value of x, substitute this value of x in any of the two equations and get the value of y. Similarly, you can find other intersections too. Calculate the lengths of respective diagonals and equate them with the area given.

Complete step-by-step solution
Let us make a diagram for the given rhombus:

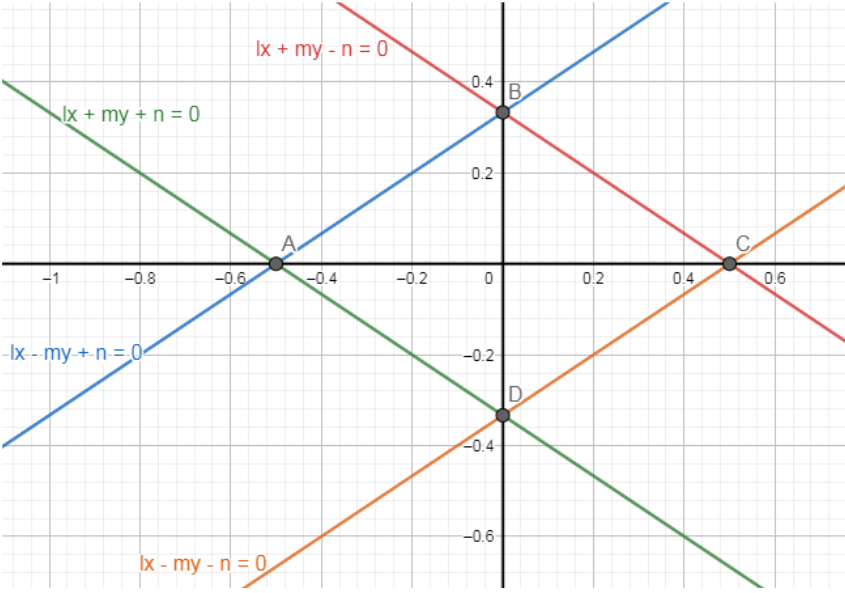
We are given four sets of lines, which make a rhombus. Now at first, we will find the coordinates of the four vertices of the rhombus.
From the diagram, it is clear which lines intersect which one. Point A is the intersection of the lines \[lx+my+n=0\] and \[lx-my+n=0\]. Now, we are going to solve these two equations:
\[lx+my+n=0\]………. Eq. (1)
\[lx-my+n=0\]………… Eq. (2)
Adding eq. (1) and eq. (2) we get,
$\begin{align}
  & lx+my+n=0 \\
 & \dfrac{lx-my+n=0}{2lx+0+2n=0} \\
\end{align}$
Writing the above equation we get,
$\begin{align}
  & 2lx+2n=0 \\
 & \Rightarrow 2lx=-2n \\
\end{align}$
Dividing 2l on both the sides we get,
$\begin{align}
  & \dfrac{2lx}{2l}=\dfrac{-2n}{2l} \\
 & \Rightarrow x=-\dfrac{n}{l} \\
\end{align}$
Substituting the above value of x in eq. (1) we get,
\[\begin{align}
  & l\left( \dfrac{-n}{l} \right)+my+n=0 \\
 & \Rightarrow -n+my+n=0 \\
 & \Rightarrow my=0 \\
 & \Rightarrow y=0 \\
\end{align}\]
From the above, we get A = \[\left( -\dfrac{n}{l},0 \right)\]
Similarly, we can find the intersections of other equations too.
Point B is the intersection of the lines \[lx+my-n=0\] and \[lx-my+n=0\]. Solving these two equations, we get B = \[\left( 0,\dfrac{n}{m} \right)\]
Point C is the intersection of the lines \[lx+my-n=0\] and \[lx-my-n=0\]. Solving these two equations, we get C = \[\left( \dfrac{n}{l},0 \right)\]
Point D is the intersection of the lines \[lx+my+n=0\] and \[lx-my-n=0\]. Solving these two equations, we get D = \[\left( 0,-\dfrac{n}{m} \right)\]
We know that distance between two points \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\] is \[\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}\]
So, length of the diagonal AC = \[\sqrt{{{(-\dfrac{n}{l}-\dfrac{n}{l})}^{2}}+{{(0-0)}^{2}}}=\left| \dfrac{2n}{l} \right|\]
So, length of the diagonal BD = \[\sqrt{{{(0-0)}^{2}}+{{\left( \dfrac{n}{m}-(-\dfrac{n}{m} \right)}^{2}}}=\left| \dfrac{2n}{m} \right|\]
We know that the area of a rhombus is half of the product of the length of diagonals. It is given that the area is 2.
So,\[\dfrac{1}{2}\cdot \left| \dfrac{2n}{l} \right|\cdot \left| \dfrac{2n}{m} \right|=2\]
\[\Rightarrow {{n}^{2}}=\left| lm \right|\]
We know that this is possible whenever l, m, n are in G.P.
Hence, the correct answer is option (a) l, m, n are in G.P

Note: Generally, students got confused while drawing the straight lines. For instance, in the above problem, we have 4 lines with 2 different slopes. The difference in slopes is just of the sign while the magnitude is the same so this is where confusion occurs.
In the below, we are going to show the two straight lines with different slopes which are given above:
\[lx+my-n=0\]
\[lx-my-n=0\]
You can avoid the mistake by separately calculating the slope of each line and then compare which is positive and which is negative. The other way to solve this problem is that whenever you see the sign of x and y in the straight line as the same then the slope is always negative and whenever you see the signs of x and y in the straight lines as different then the slope is always positive. Using this trick, the first line is of negative slope and the second line is of positive slope.