Question

If the area of the rectangle with length 32cm is equal to the area of a square with side 16cm. Find the breadth of the rectangle.

Answer 1

Hint:
* A rectangle is a geometrical four sided figure with opposite sides equal in length and adjacent sides at right angle and adjacent sides are not equal in length.
The area of the rectangle is given by \[lb\] where \[l\] is the length and \[b\] is the breadth of the rectangle.
* A square is a geometrical four sided figure with all sides equal in length and are at right angles to each other.
The area of a square is given by \[{a^2}\] where \[a\] is the side of the square.

Complete step by step solution:
Given, Length of a side of rectangle \[l\] is \[32\]cm and length of side of square \[a\] is \[16\]cm.

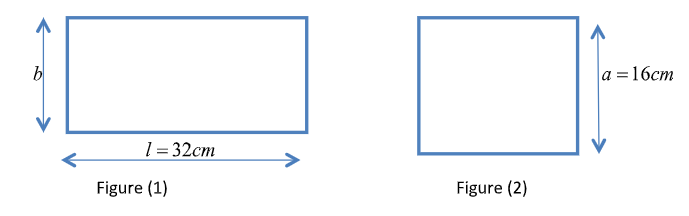
Here, Figure (1) represents the rectangle with length \[32\]cm and Figure (2) represents the square having side length \[16\]cm .
Both rectangle and square have the same area.
Find the area of the rectangle by substituting 32 for \[l\] into the formula for area, that is \[lb\].
Area of the rectangle is \[32b\] \[...(i)\]
Find the area of the square by substituting 16 for \[a\] into the formula for area, that is \[{a^2}\].
Area of the square is \[{16^2} = 256\] \[...(ii)\]
As both the areas are equal, equate the obtained areas from equation \[(i)\] and equation \[(ii)\]
\[32b = 256\]
Divide both sides by 32.
\[\dfrac{{32b}}{{32}} = \dfrac{{256}}{{32}}\]
Solve to obtain the value of \[b\].
\[b = 8\]

Therefore, the breadth of the rectangle is 8 cm.

Note:
The rectangle and parallelogram have opposite sides equal but in rectangle, the sides are at right angles to each other, although the formula for area of both is the same. Both rectangle and square have all interior angles as right angles but keep in mind the rectangle does not have all four sides equal instead it has only opposite sides equal. Students should never forget to write the S.I unit of length I.e. \[cm\] after magnitude of length and S.I unit of area i.e. \[c{m^2}\] after the magnitude of area.