Question

If the arcs of same length in two circles subtends angles \[{{65}^{\circ }}\]and \[{{110}^{\circ }}\]at the centre, find the ratio of their radii.

Answer 1

Hint: When a certain external force is applied on a pendulum, it moves back and forth with periodic motion. So it is displaced by a certain angle and it is found using the formula \[l=r\theta \]here l is arc length and “r” is radius or length of pendulum. We use the formula \[l=r\theta \].

Complete step-by-step answer:

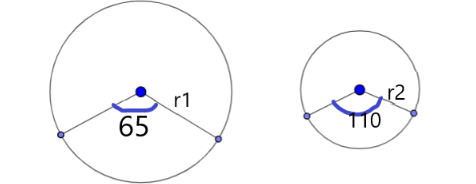
Given, the arcs of same length in two circles subtend \[{{65}^{\circ }}\]and \[{{110}^{\circ }}\]at the centre
Let the radii of two circles be \[{{r}_{1}}\]and \[{{r}_{2}}\]. Let an arc of length l subtends an angle \[{{65}^{\circ }}\]at the centre of circle of radius \[{{r}_{1}}\]
Now an arc of length l subtends an angle \[{{110}^{\circ }}\]at the centre of the circle of radius \[{{r}_{2}}\].
We know that the length of the arc is given by the formula \[l=r\theta \]

\[l=\dfrac{{{r}_{1}}13\pi }{36}\]for circle with radius \[{{r}_{1}}\]and arc length l . . . . . . . . . . . . . . . . . . . . . . . . . . . . (1)
\[l=\dfrac{{{r}_{2}}11\pi }{18}\]for circle with radius \[{{r}_{2}}\]and arc length l . . . . . . . . . . . . . . . . . . . . . . . . . . (2)
Equation (1)=equation(2)
\[\dfrac{{{r}_{1}}13\pi }{36}=\dfrac{{{r}_{2}}11\pi }{18}\]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2)
\[\Rightarrow \dfrac{{{r}_{1}}13}{2}=\dfrac{{{r}_{2}}11}{1}\]
\[\Rightarrow \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{22}{13}\]

Note: The length of the arc is given by formula \[l=r\theta \] in this \[\theta \] is the angle subtended and it is in radians but in the problem \[\theta \] is given in degrees so we have to convert to radians. To convert degrees to radians we have to multiply the given degrees with \[\dfrac{\pi }{180}\] then we will get angle subtended in radians.