Question

If the arc length and circumference of a circle are in the ratio 1:5, then the angle subtended by the arc at the centre.
A. \[{60^ \circ }\]
B. \[{72^ \circ }\]
C. \[{16^ \circ }\]
D. \[{30^ \circ }\]

Answer 1

Hint:
Here we use the concept of ratio which gives us a relation between two quantities i.e.
If we say \[m:n = 1:5\], we mean for every \[1\] \[m\] there are \[5\] \[n\]
* Ratio \[m:n = 1:5\] can be written as \[\dfrac{m}{n} = \dfrac{1}{5}\].
* The circumference of a circle is \[2\pi r\] where \[r\] is the radius of the circle and it subtends an angle of \[{360^o}\] at the centre.
* The formula for any arc on the circle is \[2\pi r\left( {\dfrac{\theta }{{360}}} \right)\] where \[\theta \] represent the angle subtended by arc on the centre.
* An arc is defined as a portion of the circumference of a circle. Since circumference is a length, so is the arc of the circle.

Complete step by step solution:

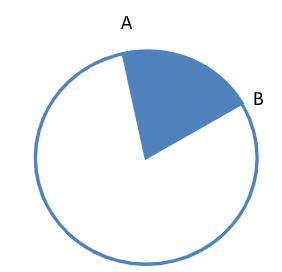
Here, Figure 1 represents a circle with Arc \[AB\]
Given, the arc length and circumference of a circle are in the ratio \[1:5\]
Arc length \[:\] Circumference \[ = 1:5\]
Since, Arc length is given by \[2\pi r\left( {\dfrac{\theta }{{360}}} \right)\] and circumference is given by \[2\pi r\].
Substitute the formula of arc length and circumference in the obtained relation.
\[\dfrac{{2\pi r\left( {\dfrac{\theta }{{360}}} \right)}}{{2\pi r}} = \dfrac{1}{5}\]
Cancel out the common factor from both denominator and numerator on the left side of the equation that is \[2\pi r\].
\[\left( {\dfrac{\theta }{{360}}} \right) = \dfrac{1}{5}\]
Multiply both sides of the equation by 360 and simplify to obtain the result.
\[
  360\left( {\dfrac{\theta }{{360}}} \right) = \dfrac{1}{5}\left( {360} \right) \\
  \theta = {72^o} \\ \]

Therefore, Option B is correct.

Note:
The angle subtended by the arc means the angle that is formed at the centre of the circle when two rays pass through the endpoints of the arc.
In these types of questions where the angle subtended at centre is to be found, the ratio of lengths is equal to the ratio of angle subtended. Students should convert the angle from degree to radian using the formula \[{1^ \circ } = \dfrac{\pi }{{180}}radians\] if it is required in the question.