Question

If the angles A, B, C, and D of a quadrilateral ABCD in the same order are in the ratio 3: 7 : 6: 4, then ABCD is a
(a) parallelogram
(b) rhombus
(c) trapezium
(d) kite

Answer 1

Hint: In order to solve this problem, we need to understand that we need to first find all the angles of the quadrilateral. In a quadrilateral, the sum of all the angles is ${{360}^{\circ }}$. Also, we must know the if two adjacent angles of the quadrilateral sum up to ${{180}^{\circ }}$, then one pair of the sides connecting these angles are parallel to each other.

Complete step-by-step solution:
We are given that the angles of the quadrilateral are in the ratio of 3: 7: 6: 4.
Let the constant of proportionality that multiplies the ratio be k.
Therefore, the angles become,
$3k, 7k, 6k, 4k.$
As these angles are the angles of the quadrilateral, we can say that with the help of the property of quadrilateral that the sum of all angles of the quadrilateral is ${{360}^{\circ }}$.
Therefore, we can write it as follows,
$3k+7k+6k+4k=360$ .
Solving this, to find the constant of proportionality k we get,
$\begin{align}
  & 20k=360 \\
 & k=\dfrac{360}{20}=18. \\
\end{align}$
Substituting the values of k in the angles, we get the angles as follows,
$3k = 3 \times 18$ = ${{54}^{\circ }}$
$7k = 7 \times 18$ = ${{126}^{\circ }}$
$6k = 6 \times 18$ = ${{108}^{\circ }}$
$4k = 4 \times 18$ = ${{72}^{\circ }}$
We are also said that the angles are in the same order.
Now, we are in a position to draw the quadrilateral ABCD.
We get the diagram as follows.

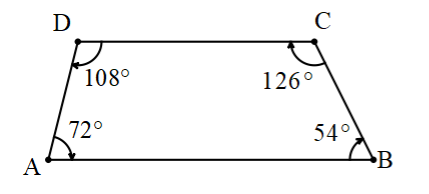
Let’s consider angle A and angle D.
The $\angle A={{72}^{\circ }}$ and $\angle D={{108}^{\circ }}$ .
Let’s add these two angles.
$\angle A+\angle D=72+108={{180}^{\circ }}$
Therefore, we can say that AB is parallel to DC.
This is due to the property of complementary angles.
The property says that when we add two angles with the common side the other two sides that make the angles are equal.
So, let's check if AD is parallel to BC.
The angles are $\angle A={{72}^{\circ }}$ and $\angle B={{54}^{\circ }}$ .
Let’s add these two angles.
$\angle A+\angle B=72+54\ne {{180}^{\circ }}$ .
Therefore, AD is not parallel to BC.
In this quadrilateral only one side is parallel.
Therefore, we can say that the quadrilateral is a trapezium.
Hence, the correct option is (c).

Note: In this problem, we need to understand that the property of complementary angles in order to identify the quadrilateral. In this property, the shape form is usually a “C” shape. We need to check whether the sum of angles is ${{180}^{\circ }}$. Also, when we find the angles of all the angles were different. But in rhombus and parallelogram, opposite angles are equal. So, we can eliminate the option (a) and (b).