Question

If the angle between two tangents drawn from an external point $P$ to a circle of radius $r$ and center $O$ is ${60^\circ }$ then find the length of $OP$.

Answer 1

Hint: We have given a circle with radius and center. Then there is an external point and two tangents drawn from the external point and the angle between two tangents is given. In this problem students are asked to find the length between the center of the circle and the external point.

Formula used: $\sin \theta = \dfrac{{{\text{opposite side}}}}{{{\text{Hypotenuse}}}}$

Complete step-by-step answer:
Given that, $P$ be the external point, $O$ be the center of the circle, $r$ be the radius of the circle.

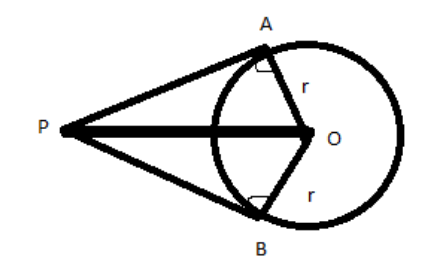
Let $A{\text{ and }}B$ be the two tangents drawn from the external point $P$ and angle between the two tangents from $P$ to the circle is ${60^\circ }$
That is, $\angle APB = {60^\circ }$
Now our aim is to claim the length of$OP$.
Now, in $\vartriangle OPA$ and $\vartriangle OPB$
$\vartriangle OAP = \vartriangle OBP$.
Since both ${90^\circ }$, as radius is perpendicular to tangent.
$OP = OP$ (Common), since $OP$ is common to both right angles $A$ and $B$
$OA = OB$, since both are radius.
$\vartriangle OPA \cong \vartriangle OPB$ (Right angle Hypotenuse Side congruency)
$\therefore \angle OPA = \angle OPB$
So, we can write $\angle OPA = \angle OPB = \dfrac{1}{2}\angle APB$
Since $\angle APB = {60^\circ }$
So, $\dfrac{1}{2}\angle APB = {30^\circ }$
$\therefore \angle OPA = {30^\circ }$
Now, in $\angle OPA$, $\sin P = \dfrac{{{\text{opposite side}}}}{{{\text{Hypotenuse}}}}$
$ \Rightarrow \sin P = \dfrac{{OA}}{{OP}}$
$ \Rightarrow \sin {30^\circ } = \dfrac{r}{{OP}}$
$\because \sin {30^\circ } = \dfrac{1}{2}$
$\therefore \dfrac{1}{2} = \dfrac{r}{{OP}}$
$ \Rightarrow OP = 2r$

The length of OP is 2r.

Note: In a right triangle, the hypotenuse is the longest side, an opposite side is the one across from a given angle, and an adjacent side is next to a given angle. The hypotenuse of a right triangle is always the side opposite the right angle. It is the longest side in a right triangle. In two right – angled triangles, if the length of the hypotenuse and one side of one triangle, is equal to the length of the hypotenuse and corresponding side of the triangle, then the two triangles are congruent.